FIND INCREASING AND DECREASING INTERVALS FOR SQUARE ROOT FUNCTION

To find increasing or decreasing interval for a square root function, we have to follow the procedure given below.

Step 1 :

Find the domain. To find domain, we have to fix the radicand ≥ 0 and solve for x.

Step 2 :

It is necessary to remember the parent graph of the square root function √x.

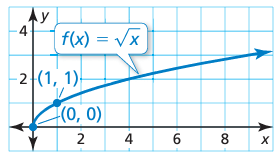
Step 3 :

Make sure is there any reflection.

The given square root function can be considered as

a - Vertical stretch / compression by the factor of a

• If a > 1, then vertical stretch
• If 0 < a < 1, then vertical compression.

b - Horizontal stretch / compression by the factor of b.

• If b > 1, then horizontal compression
• If 0 < b < 1, then horizontal stretch.

h - Horizontal move towards left or right

• If h is positive,  then move right of h units
• If h is negative, then move left of h units.

k - Vertical move towards up or down.

• If k is positive,  then move up k units.
• If h is negative, then move down k units

Note :

Sign of a and b will decide if there is any reflection or not. 

• If a is negative, then reflection across x-axis
• If b is negative, then reflection across y-axis.

Is the function increasing or decreasing on its domain and describe the transformations from the graph of f (x) = √x to the graph of h. Then graph h.

Problem 1 :

Increasing in the interval  [1, ∞).

Solution :

h(x) = 4√(x - 1)

Domain :

√(x - 1) ≥ 0

x - 1 ≥ 0

x ≥ 1

Domain is [1, ∞).

Increasing / decreasing interval :

There is no reflection, then as x increase the value of y will also increase. It must be increasing function in the interval [1, ∞).

Graphing h(x) :

Here a = 4 > 1, then vertical stretch of 4 units.

h = 1, then horizontal move 1 unit to the right. Then the starting point of the function is (1, 0).

By applying some random values of x, we draw the graph.

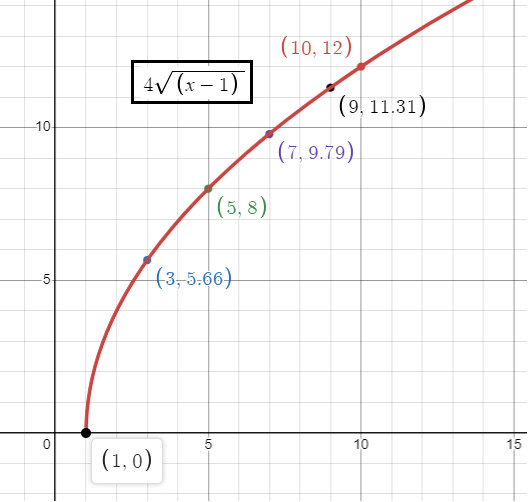
Problem 2 :

Solution :

h(x) = 2√-x - 6

Domain :

√-x ≥ 0

-x ≥ 0

x ≤ 0

Domain is (-∞, 0].

Increasing / decreasing interval :

b is negative, reflection across y-axis. Decreasing in the interval (-∞, 0].

Graphing h(x) :

Here a = 2 > 1, then vertical stretch of 2 units.

k = -6, then vertical move of 6 units down. Then the starting point of the function is (0, -6).

By applying some random values of x, we draw the graph.

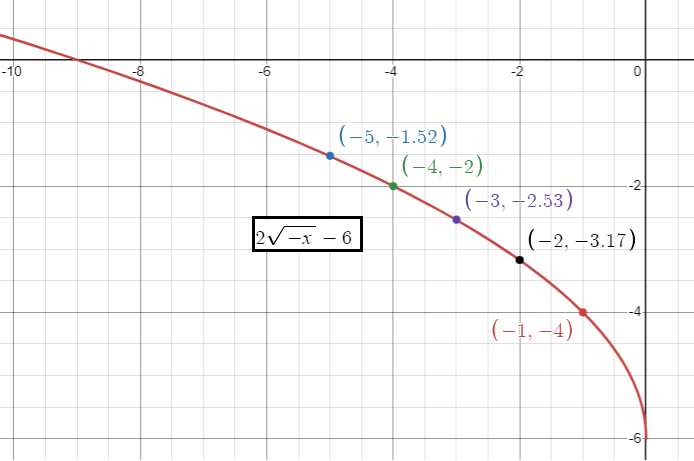
Problem 3 :

Solution :

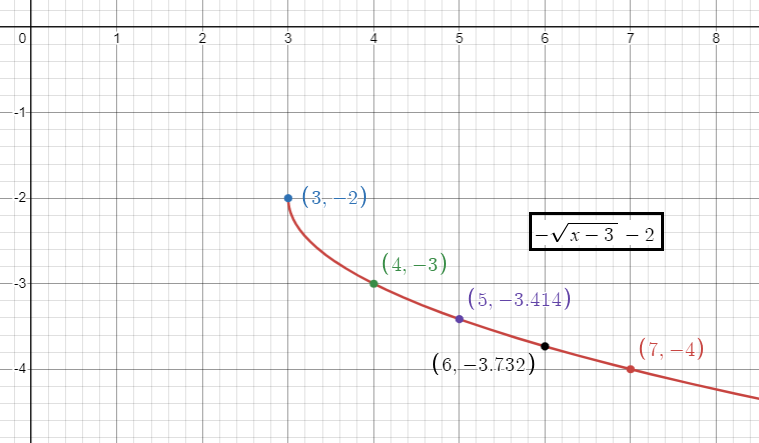
h(x) = -√(x - 3) - 2

Domain :

√(x - 3) ≥ 0

x ≥ 3

Domain is [3, ∞).

Increasing / decreasing interval :

a is negative, reflection across x-axis. Decreasing in the interval [3, ∞).

Graphing h(x) :

There is no stretch or shrink. 

h = 3, horizontal move of 3 units to the right and k = -2, then vertical move of 2 units down.

By applying some random values of x, we draw the graph.