FIND HEIGHT OF CYLINDER GIVEN SURFACE AREA

Work out the height of each cylinder below.

Problem 1 :

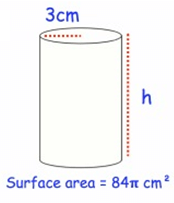
Solution :

Radius r = 3 cm, Height h = ?

Surface area (A) = 84π cm²

Surface area (A) = 2πr (h + r)

84π = 2π(3) (h + 3)

84π = 6π(h + 3)

Divide each side by 6π.

84π/6π = (6π(h + 3))/6π

14 = h + 3

14 – 3 = h

11 cm = h

Problem 2 :

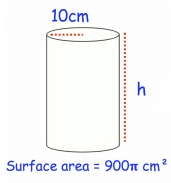
Solution :

Radius r = 10 cm and Height h = ?

Surface area A = 900π cm²

Surface area A= 2πr(h + r)

900π = 2π(10)(h + 10)

900π = 20π(h + 10)

Divide each side by 20π.

900π/20π = (20π(h + 10))/20π

45 = h + 10

45 – 10 = h

35 cm = h

Work out the radius of each cylinder below

Problem 3 :

If a cylinder has a surface area of 100 cm² and its height is 4 times the radius, what is the height of the cylinder ?

Solution :

Surface area of cylinder = 100 cm²

height = 4 (radius)

h = 4r

2πr(h + r) = 100

2πr(4r + r) = 100

2πr(5r) = 100

10πr² = 100

r² = 10/π

r = √(10/π)

height = 4√(10/π)

Problem 4 :

The radius and height of a cylinder are in the ratio 11 : 7. If the curved surface area of cylinder is 121 square cm. Find the radius and height of the cylinder.

Solution :

Radius of the cylinder = 11x and height of the cylinder = 7x

Surface area of cylinder = 121

2πrh = 121

2π 11x 7x = 121

Problem 5 :

The lateral surface area of a right circular cylinder of radius 3 cm is 94.2 cm². The height of the cylinder is ?

Solution :

Lateral surface area of cylinder = 94.2 cm²

2πrh = 94.2

2 x 3.14 x 3 x h = 94.2

h = 94.2/18.84

h = 5

So, height of the cylinder is 5 cm.