FIND EQUATION OF PARABOLA WHEN GIVEN VERTEX AND POINT WORKSHEET
Problem 1 :
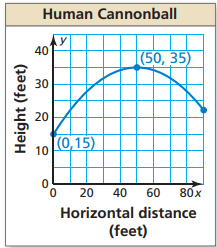
The graph shows the parabolic path of a performer who is shot out of a cannon, where y is the height (in feet) and x is the horizontal distance traveled (in feet). Write an equation of the parabola. The performer lands in a net 90 feet from the cannon. What is the height of the net?
Problem 2 :
Write an equation of the parabola that passes through the point (−1, 2) and has vertex (4, −9)
Problem 3 :
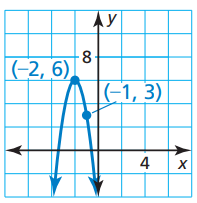
Write the equation of parabola shown in the graph below.
Problem 4 :
The graph shows the number y of students absent from school due to the flu each day x.
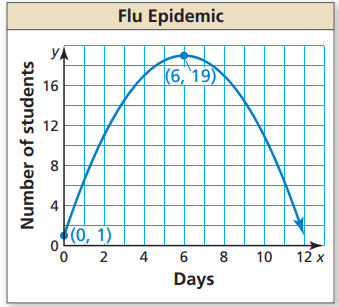
a. Interpret the meaning of the vertex in this situation.
b. Write an equation for the parabola to predict the number of students absent on day 10.
c. Compare the average rates of change in the students with the flu from 0 to 6 days and 6 to 11 days.
Answer Key
1) the height is 22.2 feet.
2) y = 0.44(x - 4)2 - 9
3) y = -3(x + 2)2 + 6
4) a) y = -(1/2)(x - 6)2 + 19
b) number of students absent on day 10 is 11 students.
c) By observing the graph, the curve is increasing from 0 days to 6 days. So, we can understand that the number of students affected is increasing. After 6 days upto 19 days since the curve is decreasing, the number of students affected is decreasing.
Problem 1 :
A parabola with vertex (1, 2) ; passes through (2, 3)
Problem 2 :
A parabola with vertex (0, -3) ; passes through (3, 0)
Problem 3 :
A parabola with vertex (-1, 4) ; passes through (-2, 3)
For each graph, write a quadratic function in vertex form and standard form.
Problem 4 :
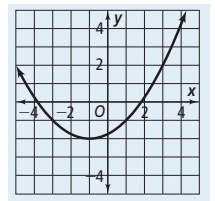
Problem 5 :
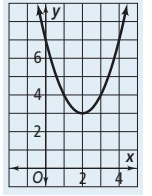
Problem 6 :
What is the equation for the parabola shown in the graph ?
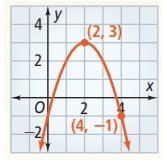
Answer Key
1) f(x) = (x – 1)2 + 2.
2) f(x) = (1/3)x2 - 3.
3) f(x) = -1(x + 1)2 + 4.
4) a)
Vertex form :
y = (1/4)(x + 1)2 – 2
b)
Standard form :
y = (1/4) (x2 + 2x – 7)
5)
a) Vertex form :
y = (x - 2)2 + 3
b) Standard form :
x2 – 4x + 7
6) f(x) = -(x – 2)2 + 3.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling