FIND EQUATION OF PARABOLA GIVEN X AND Y INTERCEPTS

Find the equation of the quadratic with graph:

Problem 1 :

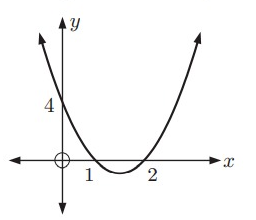
Solution:

Intercept form equation of the above parabola:

y = a(x - p)(x - q)

Because x-intercepts are (1, 0) and (2, 0).

x = 1 ---> x - 1 = 0

x = 2 ---> x - 2 = 0

Then,

y = a(x - 1)(x - 2)

It passes through (0, 4). Substitute (x, y) = (0, 4).

4 = a(0 - 1)(0 - 2)

4 = a(-1)(-2)

4 = 2a

a = 2

Intercept form equation of the parabola:

y = 2(x - 1)(x - 2)

Problem 2 :

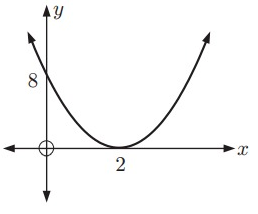
Solution:

Vertex form equation of the above parabola:

y = a(x - h)² + k

Vertex (h, k) = (2, 0)

y = a(x - 2)² + 0

y = a(x - 2)²

It passes through (0, 8). Substitute (x, y) = (0, 8).

8 = a(0 - 2)²

8 = a(-2)²

8 = 4a

a = 2

Vertex form equation of the parabola:

y = 2(x - 2)²

Problem 3 :

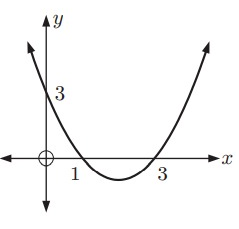
Solution:

Intercept form equation of the above parabola:

y = a(x - p)(x - q)

Because x-intercepts are (1, 0) and (3, 0).

x = 1 ---> x - 1 = 0

x = 3 ---> x - 3 = 0

Then,

y = a(x - 1)(x - 3)

It passes through (0, 3). Substitute (x, y) = (0, 3).

3 = a(0 - 1)(0 - 3)

3 = a(-1)(-3)

3 = 3a

a = 1

Intercept form equation of the parabola:

y = 1(x - 1)(x - 3)

Problem 4 :

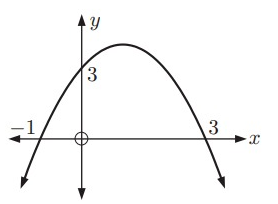
Solution:

Intercept form equation of the above parabola:

y = a(x - p)(x - q)

Because x-intercepts are (-1, 0) and (3, 0).

x = -1 ---> x + 1 = 0

x = 3 ---> x - 3 = 0

Then,

y = a(x + 1)(x - 3)

It passes through (0, 3). Substitute (x, y) = (0, 3).

3 = a(0 + 1)(0 - 3)

3 = a(1)(-3)

3 = -3a

a = -1

Intercept form equation of the parabola:

y = -1(x + 1)(x - 3)

Problem 5 :

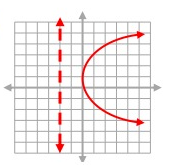
Solution:

Vertex form equation of the above parabola:

y = a(x - h)² + k

Vertex (h, k) = (1, 0)

y = a(x - 1)² + 0

y = a(x - 1)²

It passes through (0, -3). Substitute (x, y) = (0, -3).

-3 = a(0 - 1)²

-3 = a(-1)²

-3 = a

a = -3

Vertex form equation of the parabola:

y = -3(x - 1)²

Problem 6 :

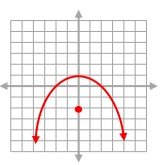
Solution:

Intercept form equation of the above parabola:

y = a(x - p)(x - q)

Because x-intercepts are (-2, 0) and (3, 0).

x = -2 ---> x + 2 = 0

x = 3 ---> x - 3 = 0

Then,

y = a(x + 2)(x - 3)

It passes through (0, 12). Substitute (x, y) = (0, 12).

12 = a(0 + 2)(0 - 3)

12 = a(2)(-3)

12 = -6a

a = -2

Intercept form equation of the parabola:

y = -2(x + 2)(x - 3)