FIND EQUATION OF CIRCLE WHEN POINT OF TANGENCY IS GIVEN

Problem 1 :

Center: (-15, 9)

Tangent to x = -17

Solution:

Given that, center (-15, 9) and tangent is x = -17

From this, we can write the point of tangency as (-17, 9). Distance between center and point of tangency will be radius.

radius = √(-15+17)² + (9 - 9)²

radius = √2²

radius = 2

Equation of circle :

(x - h)² + (y - k)² = r²

(x + 15)² + (y - 9)² = 2²

(x + 15)² + (y - 9)² = 4

x² + 30x + 225 + y² - 18y + 81 = 4

x² + y² + 30x - 18y + 225 + 81 - 4 = 0

x² + y² + 30x - 18y + 302 = 0

Problem 2 :

Center: (-2, 12)

Tangent to x = -5

Solution:

Given that, center (-2, 12) and tangent is x = -5

From this, we can write the point of tangency as (-5, 12). Distance between center and point of tangency will be radius.

radius = √(-5+2)² + (12 - 12)²

radius = √(-3)²

radius = 3

Equation of circle :

(x - h)² + (y - k)² = r²

(x + 2)² + (y - 12)² = 3²

x² + 4x + 4 + y² - 24y + 144 = 9

x² + y² + 4x - 24y + 4 + 144 - 9 = 0

x² + y² + 4x - 24y + 139 = 0

Problem 3 :

Center lies on the x-axis, tangent to x = 7 and x = -13

Solution :

Tangent can drawn through the point on the circle. The tangent lines that we draw are vertical lines. The center lies on the x-axis.

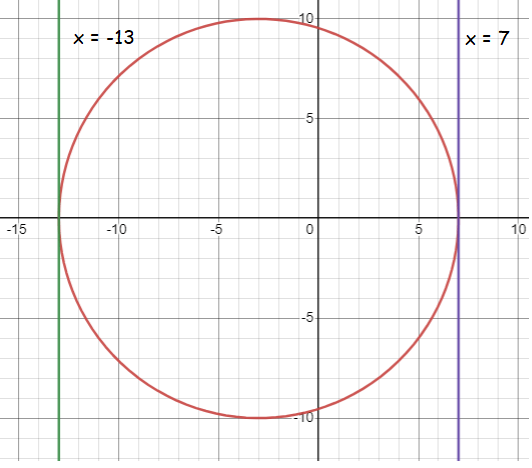
Distance between the above points = diameter

diameter / 2 = radius

Diameter = √(-13 - 7)²

= √(-20)²

= 20

Radius = 10

Midpoint of the points of tangency = center of the circle.

Since the center lies on the x-axis, the y-coordinate will be 0. Finding x-coordinate of the midpoint using the points x = -13 and x = 7.

= (-13 + 7)/2

= -6/2

= -3

So, the center is at (-3, 0).

(x - h)² + (y - k)² = r²

(x + 3)² + (y - 0)² = 10²

(x + 3)² + y² = 100

Problem 4 :

Center lies in the fourth quadrant, tangent to x = 7, y = -4 and x = 17

Solution :

The tangent lines drawn are vertical lines, then those are two end points of the circle.

y = -4 is the horizontal line

Distance between the tangents x = 7 and x = 17 is the diameter.

= 17 - 7

= 10

radius = 10/2 ==> 5

x-coordinate of midpoint from the endpoint of the diameter

= (7 + 17)/2

= 24/2

= 12

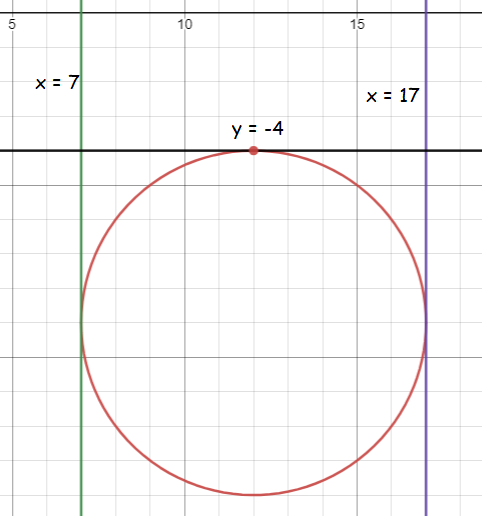
Center of the circle is (12, -4). x-coordinate of center is x = 12

(x - h)² + (y - k)² = r²

(12 - 12)² + (-4 - k)² = 5²

16 + 8k + k² = 25

k²+ 8k + 16 - 25 = 0

k²+ 8k - 9 = 0

(k + 9)(k - 1) = 0

k = -9 and k = 1