FIND EQUATION OF CIRCLE FROM GRAPH

Write down the equations of each of the circles shown below :

Problem 1 :

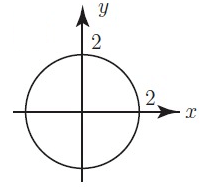
Solution :

Centre = (0, 0)

Radius r = 2

Equation of a circle is x² + y² = r²

x² + y² = 2²

x² + y² = 4

So, equation of a circle is x² + y² = r².

Problem 2 :

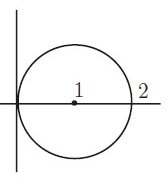
Solution :

Centre = (1, 0) and Radius r = 1

(h, k) = (1, 0)

Equation of a circle is (x – h)² + (y – k)² = r²

(x – 1)² + (y – 0)² = 1

x² + 1² - 2(x)(1) + y² = 1

x² + 1 - 2x + y² = 1

x² + y² - 2x + 1 = 1

x² + y² - 2x = 0

So, equation of a circle is x² + y² – 2x = 0.

Problem 3 :

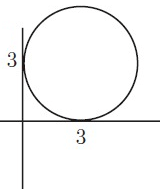
Solution :

Centre = (3, 3) and Radius r = 3

(h, k) = (3, 3)

Equation of a circle is (x – h)² + (y – k)² = r²

(x – 3)² + (y – 3)² = 3²

x² + 3² - 2(x)(3) + y² + 3² - 2(y)(3) = 9

x² + 9 – 6x + y² + 9 - 6y = 9

x² + y² – 6x – 6y + 18 = 9

Subtract 9 from both sides.

x² + y² – 6x – 6y + 18 - 9 = 9 – 9

x² + y² – 6x – 6y + 9 = 0

So, equation of a circle is x² + y² – 6x – 6y + 9 = 0.

Problem 4 :

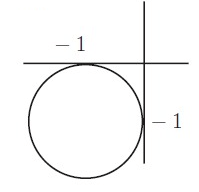
Solution :

Centre = (-1, -1) and Radius r = 1

(h, k) = (-1, -1)

Equation of a circle is (x – h)² + (y – k)² = r²

(x + 1)² + (y + 1)² = 1²

x² + 1² + 2(x)(1) + y² + 1² + 2(y)(1) = 1

x² + 1 + 2x + y² + 1 + 2y = 1

x² + y² + 2x + 2y + 2 = 1

x² + y² + 2x + 2y + 1 = 0

So, equation of a circle is x² + y² + 2x + 2y + 1 = 0.

Write down the equations of the following circles :

Problem 5 :

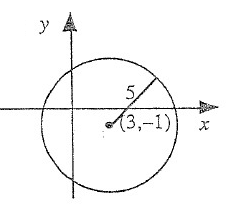
Solution :

Centre = (3, -1) and Radius r = 5

(h, k) = (3, -1)

Equation of a circle is (x – h)² + (y – k)² = r²

(x – 3)² + (y + 1)² = 5²

x²  + 3² – 2(x)(3) + y² + 1² + 2(y)(1) = 25

x² + 9 – 6x + y² + 1 + 2y = 25

x² + y² - 6x + 2y + 10 = 25

x² + y² - 6x + 2y - 15 = 0

So, equation of a circle is x² + y² - 6x + 2y - 15 = 0.

Problem 6 :

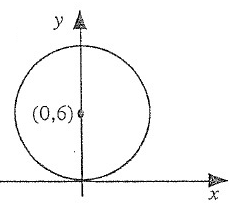
Solution :

Centre = (0, 6) and Radius r = 6

(h, k) = (0, 6)

Equation of a circle is (x – h)² + (y – k)² = r²

(x – 0)² + (y - 6)² = 6²

x²  + 0² – 2(x)(0) + y² + 6² - 2(y)(6) = 36

x² + 0 – 0x + y² + 36 - 12y = 36

x² + y² - 12y + 36 = 36

x² + y² - 12y = 0

So, equation of a circle is x² + y² - 12y = 0.

Problem 7 :

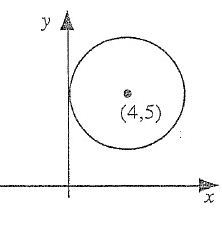
Solution :

Centre = (4, 5) and Radius r = 4

(h, k) = (4, 5)

Equation of a circle is (x – h)² + (y – k)² = r²

(x – 4)² + (y - 5)² = 4²

x²  + 4² – 2(x)(4) + y² + 5² - 2(y)(5) = 16

x²  + 16 – 8x + y² + 25 - 10y = 16

x²  – 8x + y² - 10y + 16 - 16 + 25 = 0

x²  – 8x + y² - 10y + 25 = 0

So, equation of a circle is x² + y² – 8x - 10y + 25 = 0.