FIND CRITICAL NUMBERS OF A FUNCTION

To find critical numbers, we have to use steps given below.

Step 1 :

Find the first derivative.

Step 2 :

Equate the first derivative to 0.

Step 3 :

Solve for the variable. From this, we can understand that slope will be zero at these positions.

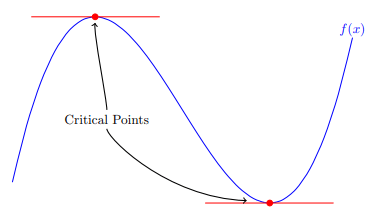
Find any critical numbers of the function.

Problem 1 :

f(x) = x³ - 3x²

Solution :

f(x) = x³ - 3x²

f'(x) = 3x² - 6x

3x² - 6x = 0

3x(x - 2) = 0

3x = 0 and x - 2 = 0

x = 0 and x = 2

So, the critical numbers are x = 0 and x = 2.

Problem 2 :

g(x) = x⁴ - 4x²

Solution :

g(x) = x⁴ - 4x²

g'(x) = 4x³ - 8x

4x³ - 8x = 0

4x(x² - 2) = 0

4x = 0 and x² - 2 = 0

x = 0 and x² = 2

x = ±√2

So, the critical numbers are x = ±√2.

Problem 3 :

g(t) = t√(4 - t), t < 3

Solution :

So, the critical numbers are t = 8/3.

Problem 4 :

Solution :

(x² + 1)(4) - (4x)(2x) = 0

4x² + 4 - 8x² = 0

-4x² + 4 = 0

-4(x² - 1) = 0

x² = 1

x = ±1

So, the critical numbers are x = 1 or -1.

Problem 5 :

h(x) = sin²x + cos x

0 < x < 2π

Solution :

h(x) = sin²x + cos x

h'(x) = 2 sin x cos x - sin x

h'(x) = 0

2 sin x cos x - sin x = 0 

sin x(2 cos x  - 1) = 0

If we solve we get,

sin x = 0 and 2 cos x - 1 = 0

x = 0 and 2 cos x = 1

cos x = 1/2

The cos of the function is positive. General solution for the cosine function

x = 2nπ ± θ where θ ∈ (0, π]

For π/3,

So, the critical numbers is x = π/3, 5π/3.

Problem 6 :

f(θ) = 2 sec θ + tan θ 

0 < θ < 2π

Solution :

f(θ) = 2 sec θ + tan θ 

f'(θ) = 2 sec θ tan θ + sec²θ

f'(θ) = 0

2 sec θ tan θ + sec²θ = 0

2 sin θ + 1 = 0 

sin θ = -1/2

The sin of the function is negative .

So, theta is third and fourth quadrant.

Hence, the interval 0 < θ < 2π.

So, the critical numbers is θ = 7π/6, 11π/6.