FIND AVERAGE VALUE OF PIECEWISE FUNCTION OVER AN INTERVAL

Let f(x) be a function on the interval [a,b]. If we divided our interval into n equally sized intervals and took the sample at left endpoints f(x_i), then an approximation for the average value would be given by the formula:

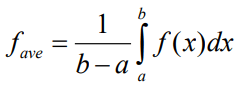
Find the average value of the function over the given interval

Problem 1 :

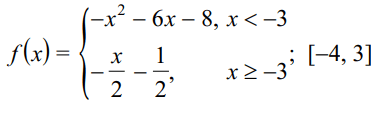
Solution :

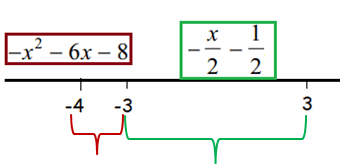
Finding average value of left piece :

f(x) = -x² - 6x - 8 on [-4, -3]

a = -4, b = -3

Finding average value of right piece :

f(x) = (-x/2) - (1/2) on [-3, 3]

a = -3, b = 3

Adding these two values,

= 0.7 + (-2)

= -0.3

So, the average value of the given function in the given interval is -0.3.

Problem 2 :

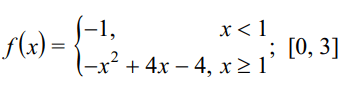
Solution :

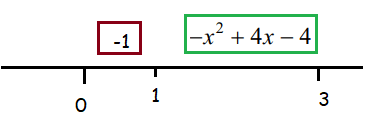
Finding average value of left piece :

f(x) = -1 on [0, 1]

a = 0, b = 1

Finding average value of right piece :

f(x) = -x² + 4x -4 on [1, 3]

a = 1, b = 3

= -1 + (-0.35)

= -1.35

So, the average value is -1.35.