FIND AMPLITUDE PERIOD PHASE SHIFT AND VERTICAL SHIFT

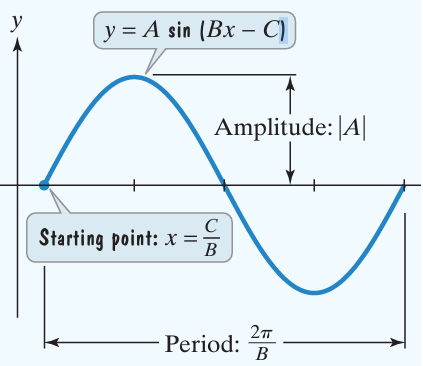
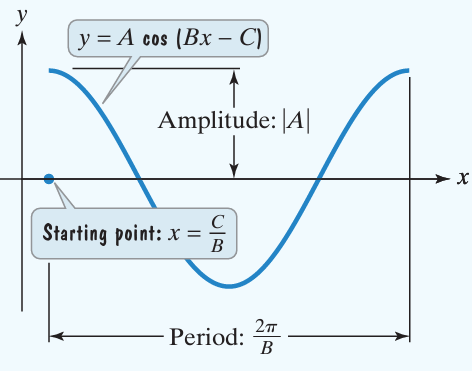
The graph of y = A sin (Bx - C) + D is obtained by horizontally shifting the graph of  y = A sin Bx so that the starting point of the cycle is shifted from x = 0 to x = C/B.

• If C/B > 0, the shift to the right 
• If C/B < 0, the shift to the left.
• If C/B is 0, then there is no phase shift.

The number C/B is called Phase shift.

Amplitude = |A|

Period = 2

• If D > 0, shift up
• If D < 0, shift down.

Determine the amplitude, period, phase shift and vertical shift for each.

Problem 1 :

Solution :

Comparing the given function with y = A sin (Bx - C) + D

A = 3, B = 4, C = -𝜋/2 and D = 2

Finding amplitude :

Amplitude = 3

Finding period :

Period = 2𝜋/|B|

= 2𝜋/4

= 𝜋/2

Finding Phase shift :

C/B = (-𝜋/2)/4

= -𝜋/8 < 0

Moving the graph towards left of 𝜋/8.

Finding vertical shift :

D = 2 > 0

Moving the graph 2 units up.

Problem 2 :

Solution :

Comparing the given function with y = A cos (Bx - C) + D

A = 2, B = 1, C = 0 and D = -4

Finding amplitude :

Amplitude = 1/2

Finding period :

Period = 2𝜋/|B|

= 2𝜋/2

= 𝜋

Finding Phase shift :

C/B = 0/2

= 0

Then there is no phase shift.

Finding vertical shift :

D = -4 < 0

Moving the graph 4 units down

Problem 3 :

Solution :

Comparing the given function with y = A cos (Bx - C) + D

A = 2, B = 1, C = 𝜋 and D = 0

Finding amplitude :

Amplitude = 2

Finding period :

Period = 2𝜋/|B|

= 2𝜋/1

= 2𝜋

Finding Phase shift :

C/B = 𝜋/1

= 𝜋 > 0

Horizontally move the graph right 𝜋.

Finding vertical shift :

D = 0

There is no vertical shift.

Problem 4 :

Solution :

Comparing the given function with y = A sin (Bx - C) + D

A = 4, B = 1, C = 𝜋 and D = -3

Finding amplitude :

Amplitude = 4

Finding period :

Period = 2𝜋/|B|

= 2𝜋/1

= 2𝜋

Finding Phase shift :

C/B = 𝜋/1

= 𝜋 > 0

Horizontally move the graph right 𝜋.

Finding vertical shift :

D = -3

Move the graph down 3 units.

Determine the amplitude, period, phase shift and vertical shift of the function. Then graph one period of the function.

Problem 5 :

Solution :

Comparing the given function with y = A cos (Bx - C) + D

A = 1, B = 1, C = 𝜋/2 and D = 0

Finding amplitude :

Amplitude = 1

Finding period :

Period = 2𝜋/|B|

= 2𝜋/1

= 2𝜋

Finding Phase shift :

C/B = (𝜋/2)/1

= 𝜋/2 > 0

Horizontally move the graph right 𝜋/2.

Finding vertical shift :

D = 0

There is no vertical shift.

Finding x-coordinates of key points :

Starting point = Period / 4

= 2𝜋/4

= 𝜋/2

Using the phase shift, starting point is 𝜋/2.

Finding y-coordinates of key points :

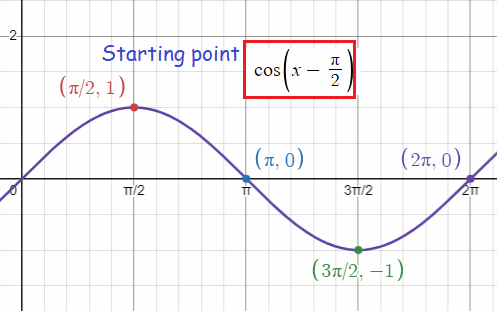
So, the points are (𝜋/2, 1) (𝜋, 0) (3𝜋/2, -1) (2𝜋, 0). Plotting the points and joining the points, we will get the curve.

Problem 6 :

Solution :

Comparing the given function with y = A sin (Bx - C) + D

A = 4, B = 2, C = 2𝜋/3 and D = 0

Finding amplitude :

Amplitude = 4

Finding period :

Period = 2𝜋/|B|

= 2𝜋/2

= 𝜋

Finding Phase shift :

C/B = (2𝜋/3)/2

= 𝜋/3 > 0

Horizontally move the graph right 𝜋/3.

Finding vertical shift :

D = 0

There is no vertical shift.

Finding x-coordinates of key points :

Each point add upto = Period / 4

= 𝜋/4

First point is x = 𝜋/3

Fifth point :

= 13𝜋/12 + 𝜋/4

= (13𝜋 + 3𝜋)/12

= 16𝜋/12

= 4𝜋/3

Finding x-coordinates of key points :

x = 𝜋/3

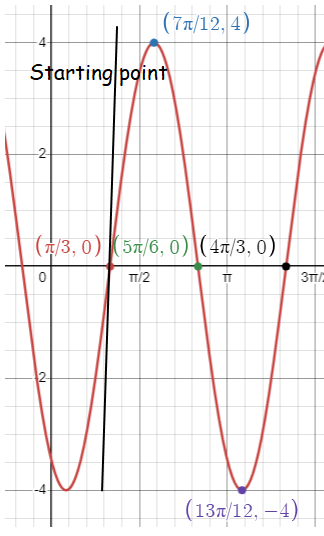
So, the points are (𝜋/3, 0) (7𝜋/12, 4) (5𝜋/6, 0) (13𝜋/12, -4) (4𝜋/3, 0). Plotting the points and joining the points, we will get the curve.