FIND ALL ZEROS OF THE POLYNOMIAL

Problem 1 :

Find all of the rational zeros of 

f(x) = 5x³ + 12x² - 29x + 12

Solution :

f(x) = 5x³ + 12x² - 29x + 12

a_n = 5 and a₀ = 12

Factor of a_0, values of p = ±1, ±2, ±3, ±4, ±6, ±12

Factor of a_n values of q = ±1, ±5

p/q =±1, ±2, ±3, ±4, ±6, ±12, ±2/5, ±3/5, ±4/5, ±6/5, ±12/5

Using synthetic division,

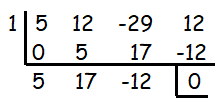
1 is the solution. To find the other two solutions, let us solve this quadratic equation got as quotient.

5x² + 17x - 12 = 0

5x² + 20x - 3x - 12 = 0

5x(x + 4) - 3(x + 4) = 0

(5x - 3) (x + 4) = 0

x = 3/5 and x = -4

So, the solutions are -4, 1 and 3/5.

Problem 2 :

f(x) = 8x⁴ + 2x³ + 5x² + 2x - 3

Solution :

Using rational root theorem, we find the possible roots for the given polynomial.

a_n = 8 and a₀ = -3

Factor of a_0, values of p = ±1, ±3

Factor of a_n values of q = ±1, ±2, ±4, ±8

p/q =±1, ±1/2, ±1/4, ±1/8, ±3/2, ±3/4, ±3/8

Using remainder theorem,

f(1) = 8(1)⁴ + 2(1)³ + 5(1)² + 2(1) - 3

= 8 + 2 + 5 + 2 - 3

≠ 0

f(-1) = 8(-1)⁴ + 2(-1)³ + 5(-1)² + 2(-1) - 3

= 8 - 2 + 5 - 2 - 3

≠ 0

f(1/2) = 8(1/2)⁴ + 2(1/2)³ + 5(1/2)² + 2(1/2) - 3

= 8(1/16) + 2(1/8) + 5(1/4) + 1 - 3

= 1/2 + 1/4 + 5/4 - 2

= (2 + 1 + 5 - 8)/4

= 0

So 1/2 is one of the solutions

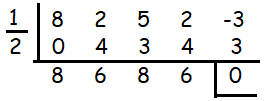
The quotient = 8x³ + 6x² + 8x + 6

Solving this quotient, we will get the remaining zeroes.

2x²(4x + 3) + 2(4x + 3) = 0

(2x² + 2)(4x + 3) = 0

2(x² + 1)(4x + 3) = 0

x = -3/4 and x = ±i

So, the solutions are 1/2, -3/4 and ±i

Problem 3 :

x³ + 4x² - 25x - 28

Solution :

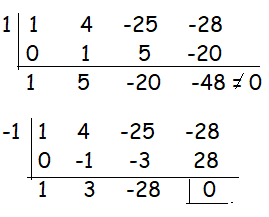
From the above synthetic division, it is clear that -1 is one of the solution.

The quotient = x² + 3x - 28 = 0

(x + 7)(x - 4) = 0

x = -7 and x = 4

So, the solution are -1, 4 and -7.

Problem 4 :

x⁴ + 2x³ - 11x² + 8x - 60

Solution :

Using rational root theorem, we find the possible roots for the given polynomial.

a_n = 1 and a₀ = -60

Factor of a_0, values of p = ±1, ±2, ±3, ±4, ±5, ±10,  ±12, ±15, ±20, ±30, ±60

Factor of a_n values of q = ±1

p/q = ±1, ±2, ±3, ±4, ±5, ±10,  ±12, ±15, ±20, ±30, ±60

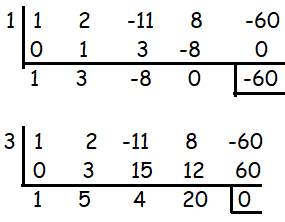
So, 3 is one of the solutions.

The quotient = x³ + 5x² + 4x + 20 = 0

x² (x + 5) + 4 (x + 5) = 0

(x² + 4) (x + 5) = 0

x² + 4 = 0 and x + 5 = 0

x = ±2i and x = -5

Problem 5 :

x³ + 6x² + 4x + 24

Solution :

Using rational root theorem, we find the possible roots for the given polynomial.

a_n = 1 and a₀ = 24

Factor of a_0, values of p = ±1, ±2, ±3, ±4, ±6, ±8,  ±12, ±24

Factor of a_n values of q = ±1

p/q = ±1, ±2, ±3, ±4, ±6, ±8,  ±12, ±24

x³ + 6x² + 4x + 24 = 0

x²(x + 6) + 4(x + 6) = 0

(x²+ 4) (x + 6) = 0

x²+ 4 = 0 and x = -6

x² = - 4

x = ±i

So, the solution -6, i and -i.

Problem 6 :

4x⁴ + 5x³ + 30x² + 45 x - 54

Solution :

Using rational root theorem, we find the possible roots for the given polynomial.

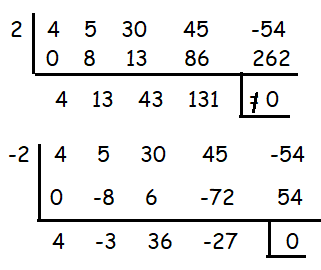
So, one of the solutions is -2.

4x³ - 3x² + 36x - 27 = 0

x²(4x - 3) + 9(4x - 3) = 0

(x²+ 9)(4x - 3) = 0

x²+ 9 = 0 and 4x - 3 = 0

x² = - 9 and x = 3/4

x = ±3i

So, the solutions are -2, 3/4, 3i and -3i