FACTORING QUADRATIC POLYNOMIALS WORKSHEET

Write each trinomial in factored form (as the product of two binomials).

Problem 1 :

p² + 14p + 48

Solution

Problem 2 :

n² + 10n + 16

Solution

Problem 3 :

p² + 14p + 40

Solution

Problem 4 :

r² + 9r + 18

Solution

Problem 5 :

p² - 8p + 7

Solution

Problem 6 :

b² - 9b + 14

Solution

Problem 7 :

b² - 8b + 15

Solution

Problem 8 :

m² - 16m + 63

Solution

Problem 9 :

k² - 4k – 60

Solution

Problem 10 :

m² + m – 6

Solution

Problem 11 :

p² - 2p – 15

Solution

Problem 12 :

r² + r – 20

Solution

Problem 13 :

The area (in square centimeters) of a square coaster can be represented by

d² + 8d + 16

a. Write an expression that represents the side length of the coaster.

b. Write an expression for the perimeter of the coaster.

Solution

Problem 14 :

The polynomial represents the area (in square feet) of the square playground.

a. Write a polynomial that represents the side length of the playground.

b. Write an expression for the perimeter of the playground.

Solution

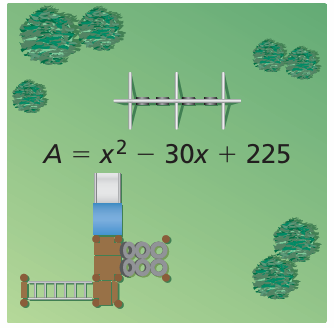
Problem 15 :

Tell whether the polynomial can be factored. If not, change the constant term so that the polynomial is a perfect square trinomial.

a. w² + 18w + 84

b. y² − 10y + 23

Solution

Problem 16 :

The width of a calculator can be represented by (3x + 1) inches. The length of the calculator is twice the width. Write a polynomial that represents the area of the calculator.

Solution

Factoring trinomials when a is not 1.

Problem 1:

7m² + 6m - 1

Solution

Problem 2 :

3k² - 10k + 7

Solution

Problem 3 :

5x² - 36x - 81

Solution

Problem 4 :

2x² - 9x - 81

Solution

Problem 5 :

3n² - 16n + 20

Solution

Problem 6 :

2r² + 7r - 30

Solution

Problem 7 :

5k² + 8k + 80

Solution

Problem 8 :

5x² - 14x + 8

Solution

Problem 9 :

7p² - 20p + 12

Solution

Problem 10 :

3v² + 14v - 49

Solution

Problem 11 :

7x² - 26x - 45

Solution

Problem 12 :

5p² - 52p + 20

Solution

Problem 13 :

The volume (in cubic feet) of a room in the shape of a rectangular prism is represented by 12z³ − 27z. Find expressions that could represent the dimensions of the room.

Solution

Problem 14 :

Factor

(a) 3x³ + 6x² − 18x

(b) 7x⁴ − 28x²

Solution

Problem 15 :

Can you use the perfect square trinomial pattern to factor y² + 16y + 64? Explain.

Solution

Problem 16 :

Which polynomial does not belong with the other three? Explain your reasoning.

a)  g² − 6g + 9      b)  n² − 4     c)  r² + 12r + 36     d)  g² + 25

Solution

Write two binomials that could represent the length and width of the rectangle.

Problem 1 :

 4x² - 7x – 2             Solution

Problem 2 :

16x² - 25         Solution

Problem 3 :

9x² - 6x + 1         Solution

Problem 4 :

3x² + 5x – 2         Solution

Problem 5 :

A projector displays an image on a wall. The area (in square feet) of the rectangular projection can be represented by x² − 8x + 15.

a. Write a binomial that represents the height of the projection.

b. Find the perimeter of the projection when the height of the wall is 8 feet.

Solution

Problem 6 :

A company’s profit (in millions of dollars) can be represented by x² − 6x + 8, where x is the number of years since the company started. When did the company have a profit of $3 million?

Solution

Problem 7 :

a. The area of the browser is 24 square inches. Find the value of x.

b. The browser covers 3/13 of the screen. What are the dimensions of the screen?

Solution

Problem 8 :

You enlarge a photograph on a computer. The area (in square inches) of the enlarged photograph can be represented by x² + 17x + 70.

a. Write binomials that represent the length and width of the enlarged photograph.

b. How many inches greater is the length of the enlarged photograph than the width? Explain.

c. The area of the enlarged photograph is 154 square inches. Find the dimensions of each photograph.

Solution