EXPONENTIAL FUNCTIONS PRACTICE PROBLEMS FOR SAT 

Problem 1 :

The population of mosquitoes in a swamp is estimated over the course of twenty weeks, as shown in the table.

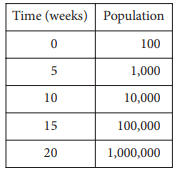
Which of the following best describes the relationship between time and the estimated population of mosquitoes during the twenty weeks?

a) Increasing linear      b) Decreasing linear

c) Exponential growth     d) Exponential decay

Solution :

By observing the inputs, it increases by 5. Gradually the inputs are increasing.

By multiplying 10 by each output, we get the next output. Since the multiplication factor is the same, it must be a exponential function.

Multiplication factor = 10 > 1

The given table will represent exponential growth function.

Problem 2 :

f (x) = 2^x + 1

The function f is defined by the equation above. Which of the following is the graph of y = −f(x) in the xy-plane?

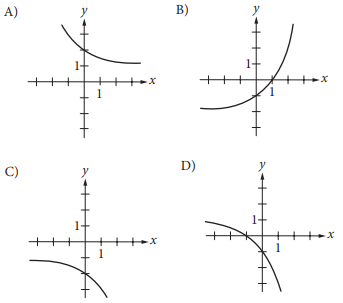
Solution :

f (x) = 2^x + 1

y = −f(x)

Represents reflection about x-axis. Let us consider the parent function as f (x) = 2^x

By applying the transformation, we have to move the graph 1 unit up. Here b = 2 > 1, then it is exponential growth function.

When x = -1, y = 2^-1 ==> 1/2

When x = 0, y = 2⁰ ==> 1

When x = 1, y = 2¹ ==> 2

(-1, 1/2) (0, 1) and (1, 2).

Points for the function f(x) = 2^x + 1

(-1, 3/2) (0, 2) and (1, 3)

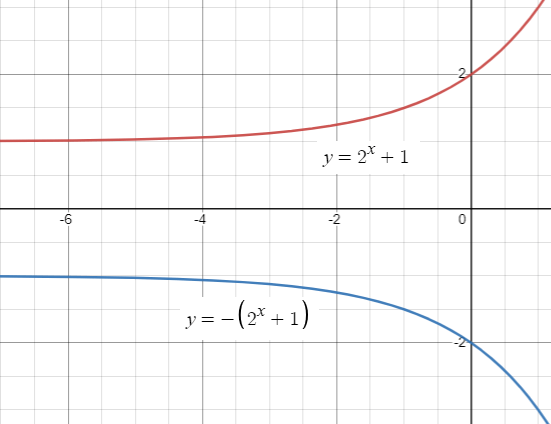
After applying reflection about y-axis, we get

- f (x) = -(2^x + 1)

So, option c is correct.

Problem 3 :

Which of the following equations relates y to x for the values in the table above?

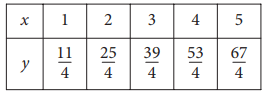
Solution :

Difference = (25/4) - (11/4) ==> 14/4

Difference = (39/4) - (25/4) ==> 14/4

Since the difference is the same, it must be a linear function

y = mx + b

Choosing two points from the table and applying, we get

(25/4) = m(2) + b

2m + b = 25/4  -----(1)

(39/4) = m(3) + b

3m + b = 39/4  -----(2)

(1) - (2)

-m = 25/4 - 39/4

-m = -14/4

m = 7/2

Applying the value of m in (1), we get

2(7/2) + b = 25/4

7 + b = 25/4

b = (25/4) - 7

b = -3/4

The required linear function will be 

y = (7/2)x - (3/4)

So, option d is correct.

Problem 4 :

The world’s population has grown at an average rate of 1.9 percent per year since 1945. There were approximately 4 billion people in the world in 1975. Which of the following functions represents the world’s population P, in billions of people, t years since 1975 ? (1 billion = 1,000,000,000)

a) P(t) = 4 (1.019)^t       b) P(t) = 4 (1.9)^t

c) P(t) = 1.19t + 4       d) P(t) = 1.019t + 4

Solution :

Rate of interest = 1.9%

It should be population growth, initial population is 4 billion.

P(t) = a(1 + r%)^t

P(t) = 4(1 + 1.9%)^t

= 4(1 + 0.019)^t

= 4(1.019)^t

So, the answer is option a.

Problem 5 :

P(t) = 60(3)^t/2

The number of microscopic organisms in a petri dish grows exponentially with time. The function P above models the number of organisms after growing for t days. Based on the function which of the following statements is true ?

a) The predicted number of organisms in the dish triples every two days.

b)  The predicted number of organisms in the dish doubles  every three days.

c)  The predicted number of organisms in the dish triples every day

d)  The predicted number of organisms in the dish doubles  every two day.

Solution :

P(t) = 60(3)^t/2

For every 2 days, the number of microscopic organisms in a petri dish triples. So, option a is correct.

Problem 6 :

P = 2000x

P = 500 (2)^x

A website administrator is considering using one of the two models above to predict the total number of purchases. P made x weeks after the website advertising campaign begins. How many more purchases are predicted by the exponential model than the linear model 5 weeks after the advertising campaign begins ? 

a)  6000        b)  8000    c)  10000    d) 18000

Solution :

From the given condition, exponential model should be greater than linear model.

500 (2)^x > 2000x

Exponential is 6000 more than the linear.

Problem 7 :

If p percent of an adult's daily allowance of potassium is provided by x servings of Crunchy Grain cereal per day, which of the following expresses p in terms of x ?

a) p = 0.5x        b)  p = 5x       c)  p = (0.05)^x    d) p = (1.05)^x 

Solution :

The variable p represents percentage of adult.

x represents Crunchy Grain cereal per day. 

Then it must be a linear function.

p = 5x

Option b is correct.