EXAMPLES OF SOLVING RATIONAL INEQUALITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Solve the following rational inequalities.
Example 1 :
(x + 6) / (x² - 5x - 24) ≥ 0
Solution :
Let f(x) = (x + 6) / (x² - 5x - 24)
f(x) ≥ 0
(x + 6) / (x² - 5x - 24) ≥ 0
(x + 6) / (x - 8) (x + 3) ≥ 0
By equating the numerator and denominator to zero, we get
x + 6 = 0, x - 8 = 0 and x + 3 = 0
x = -6, x = 8 and x = -3
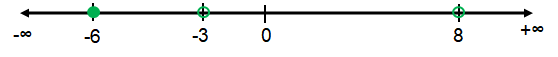
|
Intervals |
choosing value f(x) from intervals |
f(x) |
|
(-∞, -6] |
-7 Є (-∞, -6] |
f(x) ≤ 0 |
|
[-6, -3) |
-4 Є [-6, -3) |
f(x) ≥ 0 |
|
(-3, 8) |
0 Є (-3, 8) |
f(x) ≤ 0 |
|
(8, ∞) |
9 Є (8, ∞) |
f(x) ≥ 0 |
From the above, the possible values of x are
-6 ≤ x < -3 (or) x > 8
By writing it as interval notation, we get
[-6, -3) υ (8, ∞)
So, the required solution is [-6, -3) υ (8, ∞)
Example 2 :
-10/(x - 5) ≥ -11/(x - 6)
Solution :
-10/(x - 5) ≥ -11/(x - 6)
Add 11/(x - 6) on both sides,
-10/(x - 5) + 11/(x - 6) ≥ -11/(x - 6) + 11/(x - 6)
-10/(x - 5) + 11/(x - 6) ≥ 0
Let f(x) = -10/(x - 5) + 11/(x - 6)
f(x) ≥ 0
[-10(x - 6) + 11(x - 5)] / (x - 5)(x - 6) ≥ 0
[(-10x + 60) + (11x - 55)]/(x - 5)(x - 6) ≥ 0
(-10x + 60 + 11x - 55)/(x - 5)(x - 6) ≥ 0
(x + 5)/(x - 5)(x - 6) ≥ 0
By equating
the numerator and denominator to zero, we get
x + 5 = 0, x - 5 = 0, and x - 6 = 0
x = -5, x = 5, and x = 6
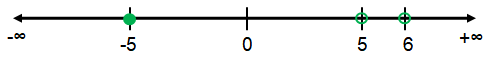
|
Intervals |
choosing value f(x) from intervals |
f(x) |
|
(-∞, -5] |
-6 Є (-∞, -5] |
f(x) ≤ 0 |
|
[-5, 5) |
0 Є [-5, 5) |
f(x) ≥ 0 |
|
(5, 6) |
5.5 Є (5, 6) |
f(x) ≤ 0 |
|
(6, ∞) |
7 Є (6, ∞) |
f(x) ≥ 0 |
From the above, the possible values of x are
- 5 ≤ x < 5 (or) x > 6
By writing it as interval notation, we get
[-5, 5) υ (6, ∞)
So, the required solution is - 5 ≤ x < 5 or x > 6.
Example 3:
-3/(x + 7) ≤ -4/(x + 8)
Solution:
-3/(x + 7) ≤ - 4/(x + 8)
Add 4/(x + 8) on both sides,
-3/(x + 7) + 4/(x + 8) ≤ - 4/(x + 8) + 4/(x + 8)
Let f(x) = -3/(x + 7) + 4/(x + 8)
-3/(x + 7) + 4/(x + 8) ≤ 0
[-3(x + 8) + 4(x + 7)] / (x + 7)(x + 8) ≤ 0
(-3x - 24 + 4x + 28) / (x + 7)(x + 8) ≤ 0
(x + 4) / (x + 7)(x + 8) ≤ 0
By equating the numerator and denominator to zero, we get
(x + 4) = 0, x + 7 = 0 and x + 8 = 0
x = -4, x = -7, and x = -8

|
Intervals |
choosing value f(x) from intervals |
f(x) |
|
(-∞, -8) |
-9 Є (-∞, -8) |
f(x) ≤ 0 |
|
(-8, -7) |
-7.5 Є (-8, -7) |
f(x) ≥ 0 |
|
(-7, -4] |
-5 Є (-7, -4] |
f(x) ≤
0 |
|
[-4, ∞) |
0 Є [-4, ∞) |
f(x) ≥ 0 |
From the above, the possible values of x are
x < -8 (or) -7 < x ≤ -4
By writing it as interval notation, we get
[-∞, -8) υ (-7, -4]
So, the required solution is [-∞, -8) υ (-7, -4]
Example 4 :
-7/(x + 5) ≤ -8/(x + 6)
Solution:
-7/(x + 5) ≤ -8/(x + 6)
Add 8/(x + 6) on both sides,
-7/(x + 5) + 8/(x + 6) ≤ -8/(x + 6) + 8/(x + 6)
-7/(x + 5) + 8/(x + 6) ≤ 0
Let f(x) = -7/(x + 5) + 8/(x + 6)
-7/(x + 5) + 8/(x + 6) ≤ 0
[-7(x + 6) + 8(x + 5)] / (x + 5)(x + 6) ≤ 0
(-7x - 42 + 8x + 40) / (x + 5)(x + 6) ≤ 0
(x - 2) / (x + 5)(x + 6) ≤ 0
By equating the numerator and denominator to zero, we get
x - 2 = 0, x + 5 = 0, and x + 6 = 0
x = 2, x = -5, and x = -6
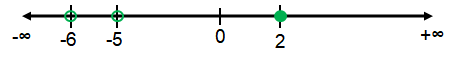
|
Intervals |
choosing value f(x) from intervals |
f(x) |
|
(-∞, -6) |
-7 Є (-∞, -6) |
f(x) ≤ 0 |
|
(-6, -5) |
-5.5 Є (-6, -5) |
f(x) ≥ 0 |
|
(-5, 2] |
0 Є (-5, 2] |
f(x) ≤
0 |
|
[2, ∞) |
3 Є [2, ∞) |
f(x) ≥ 0 |
From the above, the possible values of x are
x < -6 (or) -5 < x ≤ 2
By writing it as interval notation, we get
(-∞, -6) υ (-5, 2]
So, the required solution is x < -6 or -5 < x ≤ 2.
Example 5 :
(x + 7) (x - 3) / (x - 5)² > 0
Solution :
Let f(x) = (x + 7) (x - 3) / (x - 5)²
f(x) > 0
(x + 7) (x - 3) / (x - 5)² > 0
By equating the numerator and denominator to zero, we get
x + 7 = 0, x - 3 = 0, and (x - 5)2 = 0
x = -7, x = 3, and (x - 5)2 = 02
x = -7, x = 3, and x = 5
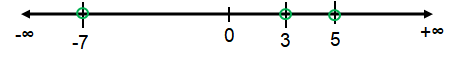
|
Intervals |
choosing value f(x) from intervals |
f(x) |
|
(-∞, -7) |
-8 Є (-∞, -7) |
f(x) > 0 |
|
(-7, 3) |
0 Є (-7, 3) |
f(x) < 0 |
|
(3, 5) |
4 Є (3, 5) |
f(x) > 0 |
|
(5, ∞) |
6 Є [5, ∞) |
f(x) > 0 |
From the above, the possible values of x are
x < -7 (or) 3 < x < 5 (or) x > 5
By writing it as interval notation, we get
(-∞, -7) υ (3, 5) υ (5, ∞)
So, the required solution is (-∞, -7) υ (3, 5) υ (5, ∞)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling