EXAMPLES OF ROTATION OF 2D SHAPES WHEN CENTER OF ROTATION IS GIVEN

If we rotate the 2d shape about origin, we will follow the rules given below about the angle that we are rotating.

Step 1 :

If center of rotation is something else than origin, we have to draw the horizontal and vertical lines in order to consider we have origin at the specified point.

Step 2 :

From the center of rotation, we have to move horizontally and vertically to get each vertices of the 2d shape.

Step 3 :

Moving right, x-coordinate = positive

Moving left, x-coordinate = negative

Moving up, y-coordinate = positive

Moving down, y-coordinate = negative

Rotating the shape means moving them around a fixed point. There are two directions

i) Clockwise

ii) Counter clockwise (or) Anti clockwise

The shape itself stays exactly the same, but its position in the space will change.

90° clockwise

90° counter clockwise

180°

270° clockwise

270° counter clockwise

(x, y) ==> (y, -x)

(x, y) ==> (-y, x)

(x, y) ==> (-x, -y)

(x, y) ==> (-y, x)

(x, y) ==> (y, -x)

Rotate each of the shapes below as instructed, using the origin, (0, 0), as the centre of rotation.

Problem 1 :

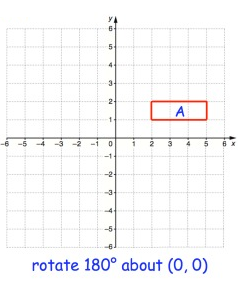
Solution:

Point A :

From P, move 2 unit right and 2 unit up. So, A(2, 2).

Point B :

From P, move 2 unit right and 1 unit up. So, B(2, 1)

Point C :

From P, 5 unit right and 1 unit up. So, C(5, 1)

Point D :

From P, 5 unit right and 2 unit up. So, D(5, 2)

Rule for 180° rotation

(x, y) ==> (-x, -y)

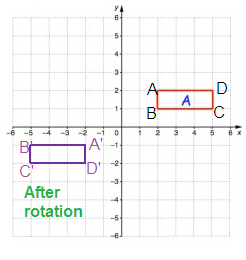
A(2, 2)

B(2, 1)

C(5, 1)

D(5, 2)

A'(-2, -2)

B'(-2, -1)

C'(-5, -1)

D'(-5, -2)

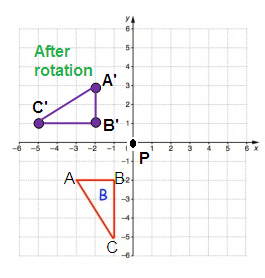
Problem 2 :

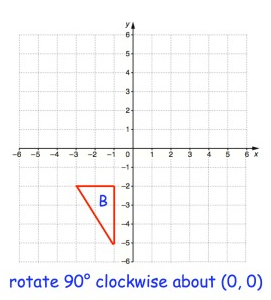
Solution:

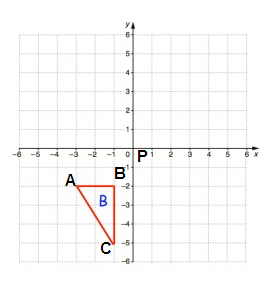
Point A:

From P, move 3 units left and 2 units down. So, A(-3, -2)

Point B:

From P, move 1 unit left and 2 units down. So, B(-1, -2)

Point C:

From P, move 1 unit left and 5 units down. So, C(-1, -5)

Rule for 90° clockwise rotation

(x, y) ==> (y, -x)

A(-3, -2)

B(-1, -2)

C(-1, -5)

A'(-2, 3)

B'(-2, 1)

C'(-5, 1)

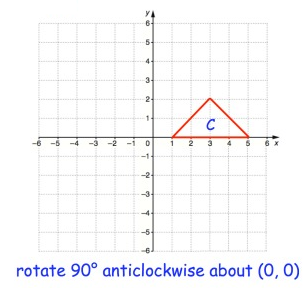
Problem 3 :

Solution:

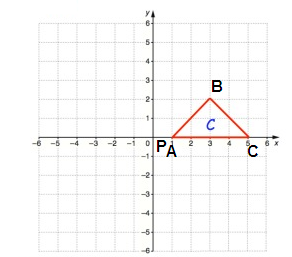
Point A:

From P, move 1 unit right and no vertical move. So, A(1, 0)

Point B:

From P, move 3 units right and 2 units down. So, B(3, 2)

Point C:

From P, move 5 units right and no vertical move. So, C(5, 0)

Rule for 90° anticlockwise rotation

(x, y) ==> (-y, x)

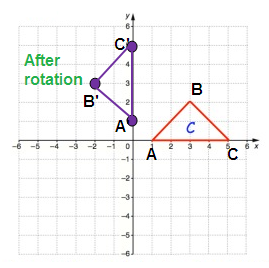
A(1, 0)

B(3, 2)

C(5, 0)

A'(0, 1)

B'(-2, 3)

C'(0, 5)

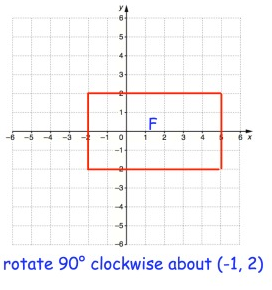
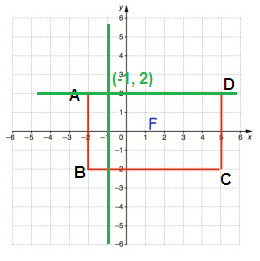
Problem 4 :

Solution:

Point A:

From P, move 4 units left and no vertical move. So, A(-1, 0)

Point B:

From P, move 1 unit left and 4 units down. So, B(-1, -4)

Point C:

From P, move 6 units right and 4 units down. So, C(6, -4)

Point D:

From P, move 6 units right and no vertical move. So, D(6, 0)

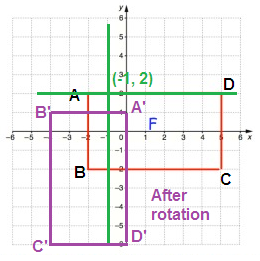
Rule for 90° clockwise rotation

(x, y) ==> (y, -x)

A(-1, 0)

B(-1, -4)

C(6, -4)

D(6, 0)

A'(0, 1)

B'(-4, 1)

C'(-4, -6)

D'(0, -6)

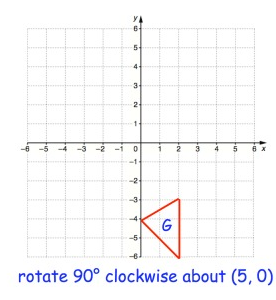
Problem 5 :

Solution:

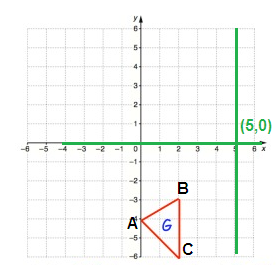
Point A:

From P, move 5 units left and 4 units down. So, A(-5, -4)

Point B:

From P, move 3 units left and 3 units down. So, B(-3, -3)

Point C:

From P, move 3 units left and 6 units down. So, C(-3, -6)

Rule for 90° clockwise rotation

(x, y) ==> (y, -x)

A(-5, -4)

B(-3, -3)

C(-3, -6)

A'(-4, 5)

B'(-3, 3)

C'(-6, 3)

EXAMPLES OF ROTATION OF 2D SHAPES WHEN CENTER OF ROTATION IS GIVEN

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling