EVALUATING PIECEWISE FUNCTIONS
Problem 1 :
Evaluate the following.

(a) 18 (b) 17 (c) 14 (d) 20
Solution :
To evaluate f(3), let us observe the functions.
The function will work only if the value of x is lesser than 2.
The function will work only if the value of x is greater than or equal to 2.
f(x) = 5x + 2
f(3) = 5(3) + 2
f(3) = 15 + 2
f(3) = 17
Problem 2 :
Evaluate for the given value.
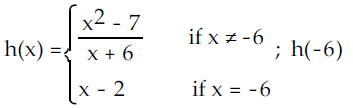
(a) -8 (b) undefined (c) 8 (d) -4
Solution :
To evaluate h(-6), let us observe the functions.
The 1st function will work only if the value of x is not equal to -6
The 2nd function will work only if the value of x is equal to -6.
h(x) = x - 2
h(-6) = -6 - 2
h(-6) = -8
Problem 3 :
Evaluate for the given value.
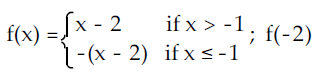
(a) -2 (b) 17 (c) 4 (d) -4
Solution :
To evaluate f(-2), let us observe the functions.
When x = -2, which is lesser than -1. So, we choose the second function.
f(x) = -(x - 2)
f(-2) = -(-2-2)
f(-2) = 4
Problem 4 :
Evaluate for the given value.
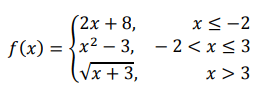
(i) f(-4) (ii) f(6) (iii) f(-2) (iv) f(0)
Solution :
|
(i) When x = -4 f(x) = 2x + 8 f(-4) = 2(-4) + 8 f(-4) = -8 + 8 f(-4) = 0 |
(ii) When x = 6 f(x) = √(x + 3) f(6) = √(6 + 3) f(6) = √9 f(6) = ±3 |
|
(iii) When x = -2 f(x) = 2x + 8 f(-2) = 2(-2) + 8 f(-2) = -4 + 8 f(-2) = 4 |
(iv) When x = 0 f(x) = x2 - 3 f(0) = 02 - 3 f(0) = - 3 |
Problem 5 :
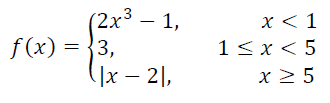
(i) f(8) (ii) f(0) (iii) f(4) (iv) f(5)
Solution :
|
(i) When x = 8 f(x) = |x - 2| f(8) = |8 - 2| f(8) = 6 |
(ii) When x = 0 f(x) = 2x3 - 1 f(0) = 2(0) - 1 f(0) = -1 |
|
(iii) When x = 4 f(x) = 3 |
(iv) When x = 5 f(x) = |x - 2| f(5) = |5 - 2| f(5) = 3 |
Problem 6 :
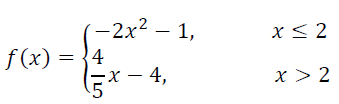
(i) f(0) (ii) f(5) (iii) f(2) (iv) f(-3)
Solution :
|
(i) When x = 0 f(x) = -2x2 - 1 f(0) = -2(0)2 - 1 f(0) = -1 |
(ii) When x = 5 f(x) = (4/5)x - 4 f(5) = (4/5)5 - 4 f(5) = 4 - 4 f(5) = 0 |
|
(iii) When x = 2 f(x) = -2x2 - 1 f(2) = -2(2)2 - 1 f(2) = -8 - 1 f(2) = -9 |
(iv) When x = -3 f(x) = -2x2 - 1 f(-3) = -2(-3)2 - 1 f(-3) = -2(9) - 1 f(-3) = -18 - 1 f(-3) = -19 |
Problem 7 :
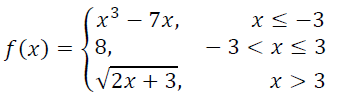
(i) f(-5) (ii) f(11) (iii) f(0) (iv) f(3)
Solution :
|
(i) When x = -5 f(x) = x3 - 7x f(-5) = (-5)3 - 7(-5) = -125 + 35 f(-5) = -90 |
(ii) When x = 11 f(x) = √(2x + 3) f(11) = √(2(11) + 3) f(11) = √(22 + 3) f(11) = √25 f(11) = ±5 |
|
(iii) When x = 0 f(x) = x3 - 7x f(0) = 03 - 7(0) f(0) = 0 |
(iv) When x = 3 f(x) = 8 f(3) = 8 |
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling