EVALUATING PIECEWISE FRUNCTIONS FROM A GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Let us consider the following,
f(a) = b
here a is input and b is output.
- Along the x-axis find the input, draw the vertical line through this point.
- The vertical line where it cuts the curve is known as output (y-value).
- If we see the transparent circle, we have to understand there is no curve. So, it will give undefined output.
- If we see the solid circle, we have to understand there is curve. So, we can mark the y-value.
Evaluate the following from the graph.
Problem 1 :
|
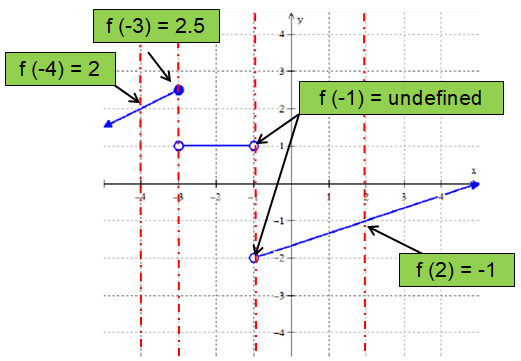
(i) 𝑓(2) = (ii) 𝑓(−3) = (iii) 𝑓(−1) = (v) 𝑓(−4) = |
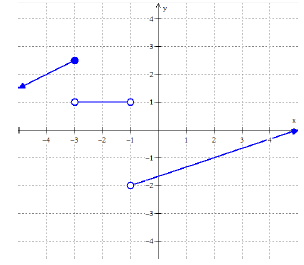 |
Solution :
Problem 2 :
Evaluate
(i) 𝑓(0) = (ii) 𝑓(−4) = (iii) 𝑓(−1) = (iv) 𝑓(3) =
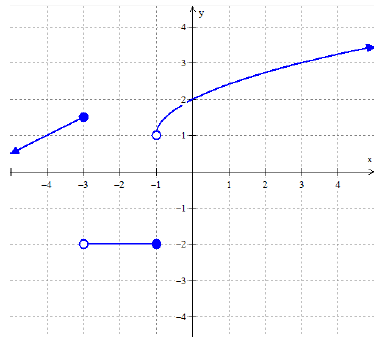
Solution :
(i) 𝑓(0) = 2
(ii) 𝑓(−4) = 1
(iii) 𝑓(−1) = -2
(iv) 𝑓(3) = 3
Problem 3 :
Evaluate the following :
a) 𝑓(−1) = b) 𝑓(2) = c) 𝑓(1) = d) 𝑓(−2) = e) f(0) =
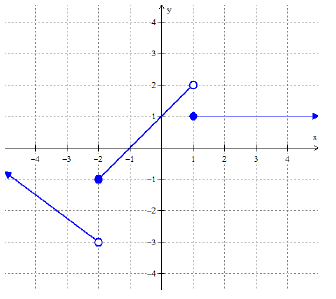
Solution :
a) 𝑓(−1) = 0
b) 𝑓(2) = 1
c) 𝑓(1) = 1
d) 𝑓(−2) = -1
e) f(0) = 1
Problem 4 :
Evaluate the following :
𝑎. 𝑓(−3) = b. 𝑓(4) = c. 𝑓(1) = d. 𝑓(−1) = e. 𝑓(0) =
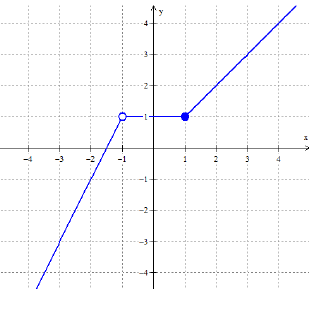
Solution :
𝑎. 𝑓(−3) = -3
b. 𝑓(4) = 4
c. 𝑓(1) = 1
d. 𝑓(−1) = undefined
e. 𝑓(0) = 1
Problem 5 :
Evaluate the following :
𝑎. 𝑓(3) = b. 𝑓(−1) = c. 𝑓(−3) = d. 𝑓(2) = e. 𝑓(0.5) =
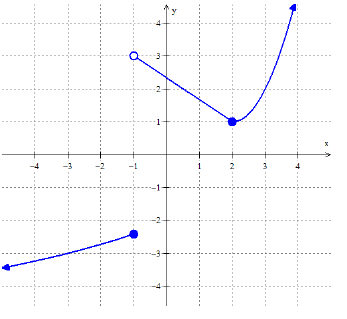
Solution :
𝑎. 𝑓(3) = 2
b. 𝑓(−1) = undefined
c. 𝑓(−3) = 3
d. 𝑓(2) = 1
e. 𝑓(0.5) = 2.5
Problem 6 :
Evaluate the following :
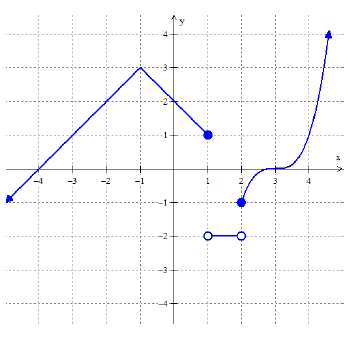
𝑎. 𝑓(−4) = b. 𝑓(1) = c. 𝑓(3) = d. 𝑓(2) = e. 𝑓(1.5) =
Solution :
𝑎. 𝑓(−4) = 0
b. 𝑓(1) = 1
c. 𝑓(3) = 0
d. 𝑓(2) = 1
e. 𝑓(1.5) = -2
Problem 7 :
If you earned upto $113700 in 2013 from an employer, your social tax rate was 6.2% of your income. If you earned over $113700, you pay a fixed amount of $7049.40
a) Write a linear piecewise function to represent the social security taxes for incomes between $0 and $500,000
b) How much scoial security tax would somone who made $50000 owe ?
c) How much money would you have made if you paid $4000 social security tax in 2013.
d) What is the meaning of f(150000)? What is the value ?
Solution :
a) Social tax to be paid in two ways, one is 6.2% of your income and the other one is fixed amount as $7049.40
Let x be the income. Then the
First piece :
6.2% of x => (6.2/100)x
= 0.062 x when 0 < x ≤ 113700
Second piece :
7049.40 when 113700 < x < 150000
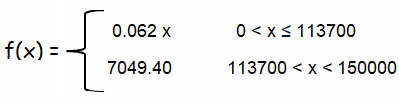
b)
When income = 50000
Amount to be paid as security tax = 0.062(50000)
= $3100
When he owe $50000, he must pay $3100 as security tax.
c)
Securiyt tax = $4000
4000 = 0.062x
x = 4000/0.062
= 64516
So, the income must be approximately $64515.
d) By evaluating f(150000), we will get to know how must we have to pay as security tax. Then
Since the income is more than 113700, he has to security tax as constant amount. That is, $7049.40.
Problem 8 :
During snow strom, a meterlogist tracks the amount of accumulating snow. For the first three hours of the strom, the snow fell at a constant rate of one inch per hour. The strom then stopped for two hours and then started again at a constant rate of one half inch per hour for next four hours.
a) create a graph of the situation
b) When will the depth of the snow be 4 inches
c) How much snow will be there be on the ground after 4 hours.
d) Write the piecewise function that models the depth of the snow as the function of time.
Solution :
Graph of first piece :
Slope = 1, y-intercept = 0
y = mx + b
y = 1x + 0
y = 1x
|
When x = 0 y = 0 |
when x = 1 y = 1 |
when x = 2 y = 2 |
when x = 3 y = 3 |
(0, 0) (1, 1) (2, 2) (3, 3)
f(x) = 1x when 0 ≤ x ≤ 3
Graph of second piece :
The strom stopped for 2 hours.
y = 3
When x = 3, 4 and 5.
f(x) = 3 when 3 < x ≤ 5
Graph of third piece :
Slope = 1/2 inch or 0.5
y = 0.5x + b
When x = 5
Go up 1 unit and right 2 unit
(5+2, 3+1) ==> (7, 4)
4 = 0.5(7) + b
4 = 3.5 + b
b = 0.5
y = 0.5x + 0.5
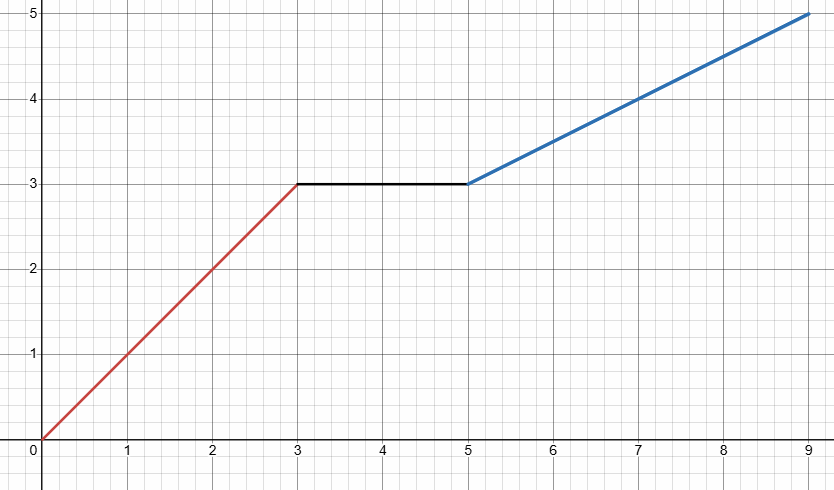
b) By observing the graph, in 7 hours the depth of the snow will be 4 inches.
c) 3 inches of snow will be there is 4 hours.
d)
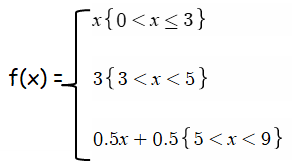
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling