EVALUATING LIMITS OF LIMITS FROM GRAPH

Give the value of each statement. If the value does not exist, write "does not exist" or "undefined".

Evaluate the following from the graph given below.

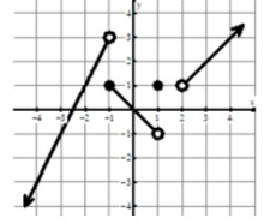
Problem 1 :

lim _x→−1^- f(x)

Solution :

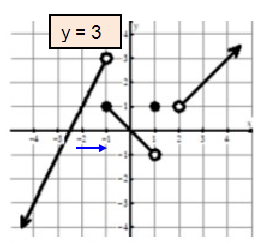
Approaching -1 from left side, we get the value of y as 3. So,

lim _x→-1^-  f(x) = 3

Problem 2 :

f(1) 

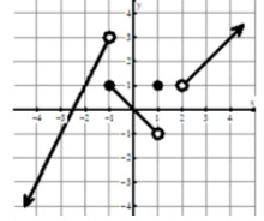
Solution :

We see the filled circle at (1, 1). So, the value of f(1) is 1.

Problem 3 :

lim _x→0 f(x)

Solution :

At exactly x approaches 0, the output is 0.

lim _x→0 f(x) = 0.

Problem 4 :

lim _x→2+ f(x)

Solution :

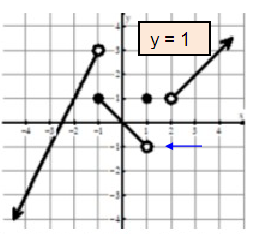
Approaching 2 from right side, the output is 1.

So, lim _x→2⁺ f(x) = 1

Problem 5 :

f(-1) 

Solution :

We see the filled circle at (-1, 1). So, the value of f(-1) is 1.

Problem 6 :

f(2) 

Solution :

f(2) = does not exists.

Problem 7 :

lim _x→−1⁺ f(x)

Solution :

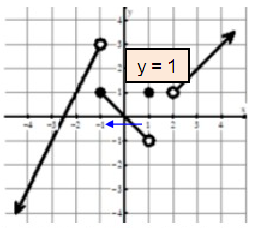
Approaching -1 from right side, we get the value of y as 1. So,

lim _x→-1⁺  f(x) = 1

Problem 8 :

lim _x→1^- f(x)

Solution :

Approaching 1 from left side, we get the value of y as -1. So,

lim _x→1^-  f(x) = -1

Problem 9 :

lim _x→2 f(x)

Solution :

Both left hand and right hand limits are not equal, the limit does not exists at x = 2.

lim _x→2  f(x) = DNE

Evaluate the following from the graph given below.

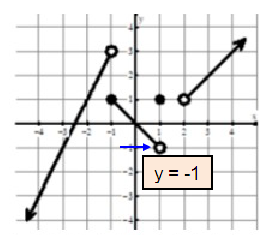
Problem 1 :

lim _x→-3 f(x)

Solution :

lim _{x →-3} f(x)

At x = -3, the curve touches the x-axis. So, the output is 0.

lim _{x →-3} f(x) = 0

Problem 2 :

f(1) 

Solution :

The point f(1) does not pass through any points. So, the answer is does not exists.

Problem 3 :

lim _x→1 f(x)

Solution :

Left  hand limits are not equal. Then right hand limit is exists at x = 1.

lim _x→1 f(x) = -5

Problem 4 :

lim _x→-2+  f(x) 

Solution :

Approaching -2 from right side, we get the value of y as 4. So,

lim _x→-2⁺  f(x) = 4

Problem 5 :

f(3) 

Solution :

The curve passes through the point (3, -1).

f(3) = -1

Problem 6 :

lim _x→-2^-f(x)

Solution :

Approaching -2 from left side, we get the value of y as 1. So,

lim _{x →-2}^-  f(x) = 1

Problem 7 :

lim _x→-2  f(x)

Solution :

Both left hand and right hand limits are not equal, the limit does not exists at x = -2.

lim _x→-2  f(x) = DNE

Problem 8 :

f(-2) 

Solution :

We see the filled circle at (-2, 3). So, the value of f(-2) is 3.

Problem 9 :

f(4) 

Solution :

The curve passes through the point (4, 1), so the value of f(4) is 1.

Evaluate the following from the graph given below.

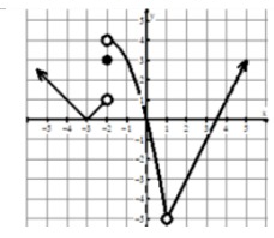
Problem 1 :

lim _x→3⁺ f(x)

Solution :

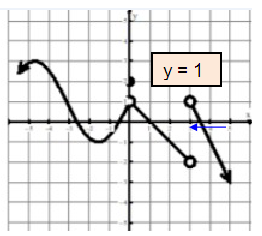
Approaching 3 from right side, we get the value of y as 1. So,

lim _x→3⁺  f(x) = 1

Problem 2 :

f(3) 

Solution : 

The curve does not pass through any points on the y-axis. So, the answer is does not exists.

Problem 3 :

lim _x→0 f(x)

Solution :

At exactly x approaches 0, the output is 1.

lim _x→0 f(x) = 1.

Problem 4 :

lim _x→3 f(x)

Solution :

Both left hand and right hand limits are not equal, the limit does not exists at x = 3.

lim _x→3  f(x) = DNE

Problem 5 :

f(0) 

Solution : 

The curve is passing through (0, 2). So, the value of f(0) is 2.

Problem 6 :

lim _x→3^- f(x)

Solution : 

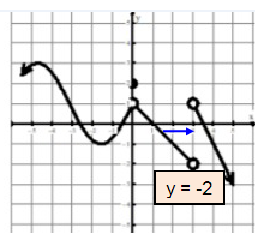
Approaching 3 from right side, we get the value of y as -2. So,

lim _x→3^-  f(x) = -2

Problem 7 :

lim _x→0⁺ f(x)

Solution :

While approaching the value 0 from left side, the output becomes 1.

So, lim _x→0+ f(x) = 1.

Problem 8 :

f(1) 

Solution : 

The curve is passing through (1, 0). So, the value of f(1) is 0.