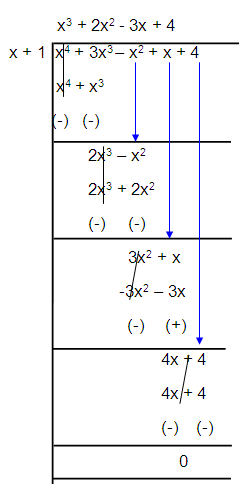EVALUATING LIMITS ALGEBRAICALLY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Evaluate the following limits without using a calculator.
Problem 1 :
Solution :
Problem 2 :
Solution :
Problem 3 :
lim x → -1 x4 + 3x3 - x2 + x + 4x + 1
Solution :
Given, lim x → -1 x4 + 3x3 - x2 + x + 4x + 1x4 + 3x3 - x2 + x + 4 ÷ (x + 1)
= lim x → -1 (x + 1) x3 + 2x2 -3x + 4x + 1= lim x → -1 x3 + 2x2 -3x + 4= (-1)3 + 2(-1)2 -3(-1) + 4= -1 + 2 + 3 + 4= 8
Problem 4 :
lim x → 0 x + 4 - 2x
Solution :
Given, lim x → 0 x + 4 - 2x = lim x → 0 x + 4 - 2x × x + 4 + 2x + 4 + 2= lim x → 0 (x + 4 - 4)xx + 4 + 2= lim x → 0 xxx + 4 + 2= lim x → 0 1x + 4 + 2= 10 + 4 + 2= 12 + 2= 14
Problem 5 :
lim x → 3 x + 6 - xx - 3
Solution :
Given, lim x → 3 x + 6 - xx - 3 = lim x → 3 x + 6 - xx - 3 × x + 6 + xx + 6 + x= lim x → 3 x + 6 - x2 (x - 3) x + 6 + x= lim x → 3 -(x - 3) (x + 2)(x - 3)x + 6 + x= lim x → 3 -(x + 2)x + 6 + x= -(3 + 2)3 + 6 + 3= -53 + 3= -56
Problem 6 :
lim x → -2 12 + 1xx + 2
Solution :
Given, lim x → -2 12 + 1xx + 2 = lim x → -2 x + 22xx + 2 = lim x → -2 x + 22x · 1x + 2= lim x → -2 12x= 12(-2)= -14
Problem 7 :
lim x → 12 x-1 - 2x - 12
Solution :
Given, lim x → 12 x-1 - 2x - 12 = lim x → 12 1x - 2x - 12 = lim x → 12 1 - 2xx 2x - 12 = lim x → 12 2(1 - 2x)x(2x - 1) = lim x → 12 -2(2x - 1)x(2x - 1) = lim x → 12 -2x= -212= -2 × 2= -4
Problem 8 :
lim x → 3 1x2 - 19x - 3
Solution :
Given,lim x → 3 1x2 - 19x - 3 = lim x → 3 9 - x29x2 x - 3 = lim x → 3 -x2 - 99x2 x - 3 = lim x → 3 -x2 - 329x2 x - 3 = lim x → 3 -(x + 3) (x - 3)9x2 x - 3 = lim x → 3 -x + 39x2= -3 + 39(3)2= -681= -227
Problem 9 :
lim x → 0 5x2 + x - 5x
Solution :
Given, lim x → 0 5x2 + x - 5x= lim x → 0 5x - 5x2 + xxx2 + x = lim x → 0 5x - 5x2 - 5xx3 + x2 = lim x → 0 -5x2x2(x + 1) = lim x → 0 -5x + 1 = -50 + 1 = -5
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.