EVALUATING COMPOSITION OF FUNCTIONS FROM TABLE WORKSHEET
Problem 1 :
Use the table of values to evaluate each expression
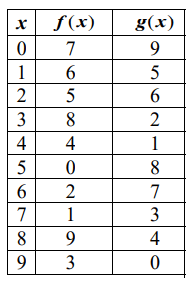
|
1) f ( g(8) ) 4) g ( f (3) ) 7) g ( g (2) ) |
2) f( g(5) ) 5) f ( f (4) ) 8) g ( g (6) ) |
3) g ( f (5) ) 6) f ( f (1) ) 9) g ( g (1) ) |
Problem 2 :
Evaluating Composite Functions :
The tables give some selected ordered pairs for functions f and g
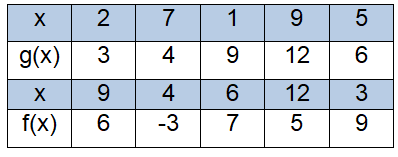
|
1) (f ∘ g)(2) 2) (f ∘ g)(1) 3) (f ∘ g)(9) |
4) (f ∘ g)(5) 5) (g ∘ f)(6) 6) (f ∘ g)(7) |
7) (g ∘ f)(12) 8) (g ∘ f)(3) |
Problem 3 :
Use the tables of ordered pairs to determine the value of each composite function

|
1) (𝑓 ∘ 𝑔)(36) = 2) (𝑔 ∘ 𝑔)(16) = |
3) (𝑔 ∘ 𝑓)(4) = 4) (𝑓 ∘ 𝑓)(4) = |
Problem 4 :
The table below shows values of 𝑓(𝑥) at selected values of 𝑥. The function 𝑔(𝑥) is shown in the graph below.
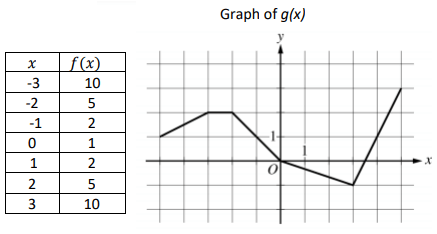
Let h be the function defined by ℎ(𝑥) = 2|𝑥 − 4|.
Find:
|
1. 𝑦 = ℎ(𝑓(2)) 2. 𝑦 = ℎ(𝑔(3)) 3. 𝑦 = 𝑔(𝑓(−2)) |
4. 𝑦 = 𝑓(𝑔(−3)) 5. 𝑦 = 𝑔(𝑓(ℎ(3))) 6. Find ℎ(𝑓(𝑔(0))) |
Use the values in the table to evaluate the indicated composition of functions.
Problem 5 :
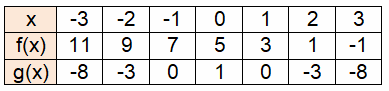
|
(i) (f ∘ g) (1) (ii) (g ∘ f) (2) (iii) (g ∘ g) (1) |
(iv) (f ∘ g) (2) (v) (g ∘ f) (3) (vi) (f ∘ f) (3) |
Problem 6 :
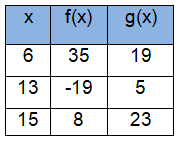
(i) f(13)
(ii) f(6)
(iii) g(15)
(iv) g(13)
(v) For what value of x, f(x) = 35 ?
(vi) For what value of x, g(x) = 5 ?
Problem 7 :
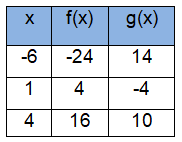
(i) f(4) =
(ii) g(1) =
(iii) g(4) =
(iv) g(-6) =
(v) For what value of x, f(x) is -24 ?
(vi) For what value of x, f(x) is 4 ?
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling