EVALUATING COMPOSITE FUNCTIONS FROM GRAPHS WORKSHEET

Problem 1 :

The first of the two graphs shows two functions 𝑓 𝑎𝑛𝑑 𝑔. The second shows two functions ℎ 𝑎𝑛𝑑 𝑘. Use the graphs to compute the following:

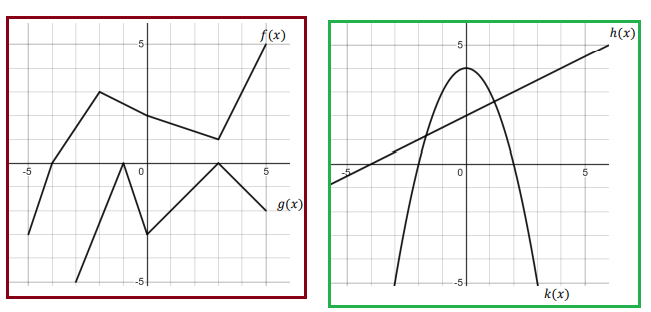
1) (𝑔 ◦ 𝑓)(−4) =

2) (𝑓 ◦ 𝑔)(3) =

3) (𝑓 ◦ 𝑓)(−2) =

4) (𝑔 ◦ 𝑔)(3) =

5) (𝑔 ◦ 𝑓)(−5) =

6) (𝑔 ◦ 𝑓)(−3) =

7) (ℎ ◦ 𝑘)(0) =

8) (ℎ ◦ 𝑘)(−1) =

9) (ℎ ◦ 𝑘)(2) =

10) (ℎ ◦ 𝑘)(−3) =

11) (𝑘 ◦ ℎ)(0) =

12) (𝑘 ◦ ℎ)(2) =

13) (𝑘 ◦ ℎ)(−4) =

14) (𝑘 ◦ ℎ)(−2) =

Solution

Problem 2 :

Refer to the graph to complete the statements below.

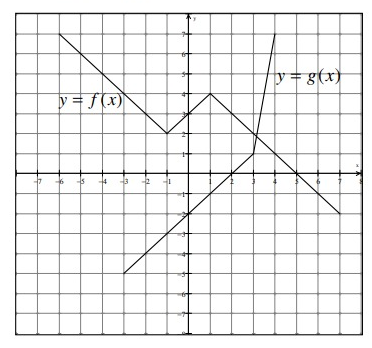
a) (f + g)(-3) = ______

b) (f · g)(2) = ______

c) (f/g)(-1) = ______

d) (f ∘ g)(3) = ______

e) g^-1(-4) = ______

f) Evaluate (f ∘ f)(2) ______

g) Evaluate g(f(g(1))) ______

h) State the domain of f + g _____

i) State the domain of f/g. ______

j) Evaluate (f(3))³ - 4g(-2) ______

k) For what value(s) is f(x) = 3? _______

Solution

Answer Key

1) (𝑔 ◦ 𝑓)(−4) = -3

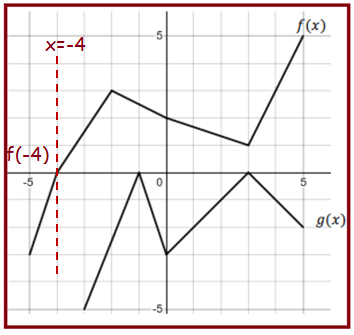
2) (𝑓 ◦ 𝑔)(3) = f[g(3)] = f[0] ==> 2

3) (𝑓 ◦ 𝑓)(−2) = f[f(-2)] = f[3] ==> 1

4) (𝑔 ◦ 𝑔)(3) = g[g(3)] = g[0] ==> -3

5) (𝑔 ◦ 𝑓)(−5) = g[f(-5)] = g[-3] ==> -5

6) (𝑔 ◦ 𝑓)(−3) = g[f(-3)] = g[1.5] ==> -1.5

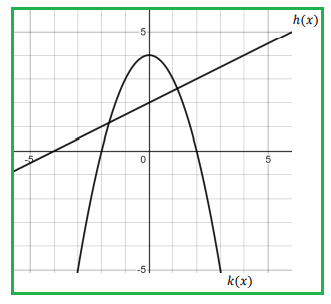
7) (ℎ ◦ 𝑘)(0) = h[k(0)] = h[4] ==> 4

8) (ℎ ◦ 𝑘)(−1) = h[k(-1)] = h[3] ==> 3.5

9) (ℎ ◦ 𝑘)(2) = h[k(2)] = h[0] ==> 2

10) (ℎ ◦ 𝑘)(−3) = h[k(-3)] = h[-5] ==> -0.5

11) (𝑘 ◦ ℎ)(0) = k[h(0)] = k[2] ==> 0

12) (𝑘 ◦ ℎ)(2) = k[h(2)] = k[3] ==> -5

13) (𝑘 ◦ ℎ)(−4) = k[h(-4)] = k[0] ==> 4

14) (𝑘 ◦ ℎ)(−2) = k[h(-2)] = k[1] ==> 3

2) a)(f + g)(-3) = -1

b) (f · g)(2) = 0

c) (f/g)(-1) = 2/(-3)

d) (f ∘ g)(3) = 4

e) x = -3

f) (f ∘ f)(2) = 2

g) g(f(g(1))) = 0

h) the domain of (f + g)(x) is [-3, 4].

i) domain of (f/g)(x) = [-3, 1] u (3, 4]

k) (f(3))³ - 4g(-2) = 24

l) x values are -2, 0 and 2.

EVALUATING COMPOSITE FUNCTIONS FROM GRAPHS WORKSHEET

Answer Key

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling