EVALUATING ALGEBRAIC EXPRESSIONS WORKSHEET

Example 1 :

a³ - [(b² + c)/a] + (ab + c), if a = 4, b = -3 and c = 7

Solution :

= a³ - [(b² + c)/a] + (ab + c)

When a = 4, b = -3 and c =-7

= 4³ - [((-3)² + 7)/4] + [(4)(-3) + 7]

= 64 - [(9 + 7)/4] + [-12 + 7]

= 64 - (16/4) + (-5)

= 64 - 4 - 5

= 55

Example 2 :

What is the value of

(2c/a)² - 10 x (b +a)/c

if a = -2, b = 3 and c = 5 ?

Solution :

= (2c/a)² - 10 x (b +a)/c

= [2(5)/-2]² - 10 x (3 - 2)/5

= (-5)² - 10 x (1/5)

= 25 - 2

= 23

Example 3 :

What is the value of

9 - 2x ÷ (z - y)³

if x = 4, y = -1 and z = -3 ?

Solution :

= 9 - 2x ÷ (z - y)³

= 9 - 2(4) ÷ (-3 + 1)³

= 9 - 8 ÷ (-2)³

= 9 - 8 ÷ (-8)

= 9 + 1 

= 10

Example 4 :

If x = 10, what is the value of x/2 + x/20 + x/200 ?

Solution :

= x/2 + x/20 + x/200

When x = 10

= 10/2 + 10/20 + 10/200

= 5 + 1/2 + 1/20

= (100+10+1)/20

= 111/20

= 5.55

Example 5 :

If a = 3, b = -1 and c = -2, what is the value of 

7 - [(a - 12) ÷ (2 - b)] / (c+ 3) ?

Solution :

= 7 - [(a - 12) ÷ (2 - b)] / (c+ 3)

= 7 - [(3 - 12) ÷ (2 +1)] / (-2+ 3)

= 7 - (-9 ÷ 3) / (-2+ 3)

= 7 - (-3)/1

= 7 + 3

= 10

Example 6 :

The sum of first n natural numbers is given by (1/2)n² + (1/2)n. Find 

a)  The sum of first 5 natural numbers.

b)  The sum of first 11 natural numbers.

c)  The sum of natural numbers from 11 to 30.

Solution :

The sum of first n natural numbers = (1/2)n² + (1/2)n

a)  The sum fo first 5 natural numbers 

= (1/2)n² + (1/2)n

Applying n = 5, we get

= (1/2) 5² + (1/2)5

= 25/2 + 5/2

= (25 + 5)/2

= 30/2

= 15

b)  The sum of first 11 natural numbers.

= (1/2)n² + (1/2)n

Applying n = 11, we get

= (1/2) 11² + (1/2)11

= 121/2 + 11/2

= (121 + 11)/2

= 132/2

= 66

c) 

The sum of 30 terms :

Applying n = 30, we get

= (1/2)30² + (1/2)30

= 900/2 + 30/2

= 930/2

= 465/2

The sum of 11 terms :

Applying n = 11, we get

= (1/2)11² + (1/2)11

= 121/2 + 11/2

= (121 + 11)/2

= 135/2

Sum of terms from 11 to 30 :

= 465/2 - 135/2

= (465 - 135)/2

= 330/2

= 165

So, the required sum is 165.

Example 7 :

After m months, the length of a finger nail is 10 + 3m millimeters. How long is the finger nail after eight months? three years?

Solution :

Length of finger nail = 10 + 3m

Length of nail after 8 months, applying m = 8

= 10 + 3(8)

= 10 + 24

= 34 mm

Length of nail after 3 years.

1 year = 12 months

3 years = 3(12)

= 36 months

Applying m = 36

= 10 + 3(36)

= 10 + 108

= 118 mm

Example 8 :

You earn 15n dollars for mowing n lawns. How much do you earn for mowing one lawn? seven lawns?

Solution :

Your earning for n lawns = 15 n

Amount you earn for one lawn = 15(1)

= $15

Amount you earn for seven lawns = 15(7)

= $105

Example 9 :

Describe and correct the error in evaluating the expression when m = 8.

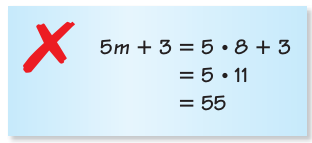
Solution :

In the expression 5m + 3, applying m = 8 we get

= 5(8) + 3

Accordingly order of operation, we have to perform multiplication first and then addition.

= 40 + 3

= 43

The error is, addition is done first and then multiplication. That is the error.

Example 10 :

You are saving for a skateboard. Your aunt gives you $45 to start and you save $3 each week. The expression 45 + 3w gives the amount of money you save after w weeks.

a. How much will you have after 4 weeks, 10 weeks, and 20 weeks?

b. After 20 weeks, can you buy the skateboard? Explain.

Solution :

Given expression is 45 + 3w

a)  Earnings after 4 weeks,

= 45 + 3(4)

= 45 + 12

= $57

Earnings after 10 weeks,

= 45 + 3(10)

= 45 + 30

= $75

Earnings after 20 weeks,

= 45 + 3(20)

= 45 + 60

= $105

b) After 20 weeks,

= 45 + 3(20)

= 45 + 60

= 105

By looking at the price, it is worth of $125. Since you have $105, you cannot purchase.