EVALUATE THE GIVEN FROM VENN DIAGRAM OF TWO SETS

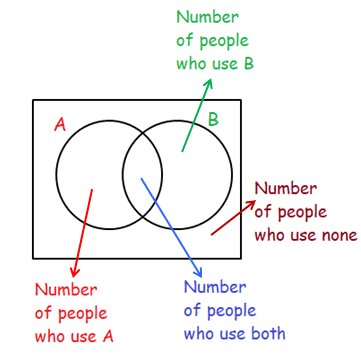
In math, Venn diagram is a method used to show the relationship between two quantities.

Each quantity will be represented in one separate circles.

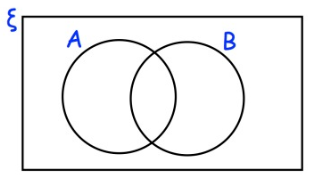
Problem 1 :

ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}

A = multiples of 3

B = multiples of 5

a) Complete the Venn diagram

One of the numbers is selected at random.

b) Write down P(A ∩ B)

Solution :

a)

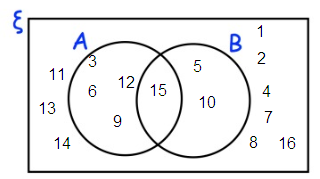
b) 

A ∩ B = {15}

So, P(A ∩ B) =1/16

Problem 2 :

Here is a Venn diagram

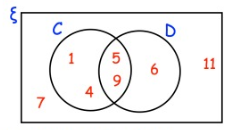
Write down the numbers that are in set

(a) D       (b)  C U D         (c) C^'

Solution :

By observing the diagram.

(a) D = {5, 6, 9}

(b) C U D = {1, 4, 5, 6, 9}

(c) C = {6, 7, 11}

Problem 3 :

At a wedding, the guests may have ice cream or custard with their dessert. The Venn diagram shows information about the choices the guests made.

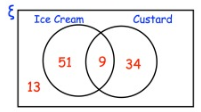
(a) How many guests had custard ?

(b) How many guests had ice cream and custard ?

(c) How many guests went to the wedding ?

Solution :

By observing the diagram.

(a)

Number of guests had custard = 9 + 34

= 43

Hence, 43 guests had custard.

(b) 9 guests had ice cream and custard.

(c)

Number of guests went to wedding

= 9 + 34 + 51 + 13

= 107

So, 8 guests went to the wedding.

Problem 4 :

Here is a Venn diagram.

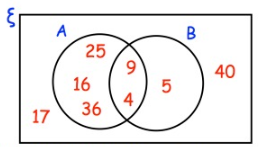
Write down the numbers that are in set

(a) A ∩ B

(b) A U B

(c) A^'

One of the numbers in the diagram is chosen at random.

(d) Find the probability that the number is in set B^'.

Solution :

(a) The variables in the common region of A and B are known as elements of A ∩ B.

A ∩ B = {4, 9}

(b) The variables inside the circles A and B are known as elements of the set A U B.

 A U B = {4, 5, 9, 16, 25, 36}

(c) 

A^' = {5, 17, 40}

(d) The number is in set B^' is not in B.

So, B^' = 5

Total number = 8

To find probability :

= 5/8

Problem 5 :

Here is a Venn diagram.

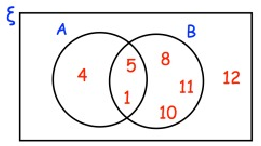
A number is chosen at random.

(a) Write down P(A ∩ B^')

(b) Write down P(A^' U B^')

(c) Write down P(B/A)

Solution :

By observing the diagram.

(a) To find  P(A ∩ B^') :

A = {1, 4, 5}

B^' = {4, 12}

A ∩ B^' = 4

P(A ∩ B^') = 1/7

(b) To find P(A^' U B^') :

A^' = {8, 10, 11, 12}

B^' = {4, 12}

A^' U B^' = {4, 8, 10, 11, 12}

P(A^' U B^') = {5/7}

(c) To find P(B/A) :

P(B/A) = P(A ∩ B)/P(A)

A ∩ B = {1, 5}

P(A ∩ B) = 2/7

P(A) = 3/7

P(B/A) = 2/7/3/7

= 2/7 × 7/3

P(B/A)  = 2/3

Problem 6 :

The Venn diagram shows information about the cars in a car park.

ξ = 150 cars in the car park

R = red cars

J = cars manufactured in Japan

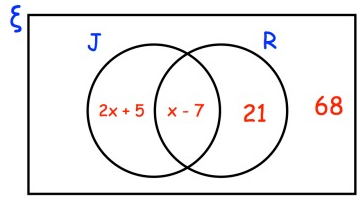
A car is chosen at random.

Work out the probability that it is red.

Solution :

150 cars in the car park.

2x + 5 + x - 7 + 21 + 68 = 150

3x + 87 = 150

3x = 63

x = 63/3

x = 21

x = 21 substitute the equation x - 7. 

= 21 - 7

= 14

21  + 14 = 35 

To find the probability :

= 35/150

= 7/30

Problem 7 :

The Venn diagram shows information about the pets owned by 40 students

ξ = 40 students

C = students who own a cat

D = students who own a dog

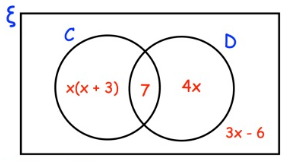
A student is chosen at random.

They own a cat.

Work out the probability that they own a dog.

Solution :

x(x + 3) + 7 + 4x + 3x - 6 = 40

x² + 3x + 7 + 4x + 3x - 6 = 40

x² + 10x + 1 = 40

x² + 10x + 1 - 40 = 0

x²  + 10x - 39 = 0

x² + 13x - 3x - 39 = 0

x(x + 13) - 3(x + 13) = 0

(x - 3) (x  + 13) = 0

x - 3 = 0 and x + 13 = 0

x = 3 and x = -13

= x(x + 3) + 7

= 3(3 + 3) + 7

= 18 + 7

= 25

They own a cat is 25.

The probability that they own a dog is 7/25.