ESTIMATION PROBLEMS WITH ONE FIGURE APPROXIMATION

What is one figure approximation ?

When estimating we usually round each number to one significant figure and evaluate the result. We call this a one figure approximation.

When estimating we usually round each number to one significant figure and evaluate the result. We call this a one figure approximation.

Rounding Two Digit Numbers

If the given number is two digit number, we have to round it to the nearest tens.

Step 1 :

To round it to the nearest tens, we have to look at the unit  digit.

Step 2 :

If the unit digit is less than 5, then we have to keep the ten's digit as it is and convert the remaining places as 0.

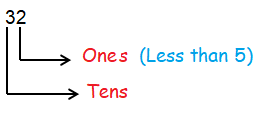
So, approximating it as 30.

If the  unit digit is greater than or equal to 5, then we have to add one with the ten's place and change the remaining digits as 0.

Approximating it as 30

Rounding Three Digit Numbers

Step 1 :

If the given number is three digit number, we have to round it to nearest hundreds and so on.

Step 2 :

To round it to the nearest hundreds, we have to look at the tens digit.

If the tens digit is lesser than 5, then we have keep the hundreds place as it is and change remaining digits as 0.

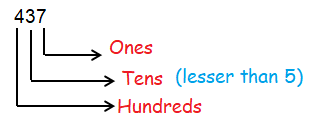
So, approximating it as 400.

If the tens digit is greater than or equal to 5, then we have to add one with the hundred's place and change the remaining digits as 0.

So, approximating it as 600.

Estimate using a one figure approximation :

Problem 1 :

22 x 394

Solution :

= 22 x 394

Rounding to one significant figure,

= 20 x 400

= 8000

Problem 2 :

218 x 74

Solution :

= 218 x 74

Rounding to one significant figure,

= 200 x 700

Problem 3 :

58 x 3102

Solution :

= 58 x 3102

Rounding to one significant figure,

= 60 x 3000

= 180000

Problem 4 :

2360 x 21

Solution :

= 2360 x 21

Rounding to one significant figure,

= 2000 x 20

= 40000

Problem 5 :

3904 x 541

Solution :

= 3904 x 541

Rounding to one significant figure,

= 4000 x 500

= 2000000

Problem 6 :

612 ÷ 29

Solution :

= 612 ÷ 29

Rounding to one significant figure,

= 600 ÷ 30

= 20

Problem 7 :

230 ÷ 54

Solution :

= 230 ÷ 54

Rounding to one significant figure,

= 200 ÷ 50

= 4

Problem 8 :

64183 ÷ 595

Solution :

= 64183 ÷ 595

Rounding to one significant figure,

= 60000 ÷ 600

= 100

Problem 9 :

27830 ÷ 426

Solution :

= 27830 ÷ 426

Rounding to one significant figure,

= 28000 ÷ 400

= 70

Problem 10 :

Hong Kong has an area of 1104 km². An average of 6349 people live in each square kilometer. Estimate the total population of Hong Kong.

Solution :

Total area of Hong Kong = 1104 km²

Average number of people live in 1 square kilometer = 6349

Total population = 1104 x 6349

Since we are estimating the population, we can round for one significant figure.

= 1000 x 6000

= 6000000 people

So, the total population of Hong Kong is 6000000 people.

Problem 11 :

There are 29 students in a class. Each student has an average of 11 books. Estimate the total number of books.

Solution :

Number of students in the class = 29

Number of books on average = 11

Total number of books = 29 x 11

Approximating to one significant figure, we get

= 30 x 10

= 300

So, the total number of books is 300.

Problem 12 :

The teacher spends a total of 292 minutes making these 12 assignments. Estimate using a one figure approximation, the average time spent making each assignment.

Solution :

Time spent for making assignments = 292

Number of assignments making = 12

Time taken to make each assignment = 292 ÷ 12

Rounding to one significant figure, we get

= 300 ÷ 10

= 30 minutes

So, time spent for making each assignment is 30 minutes.

Problem 13 :

559 eggs are divided equally between 43 baskets. Estimate the number of eggs in each basket.

Solution :

Number of eggs to be divided = 559

Number of baskets available = 43

Number of eggs in each basket = 559 ÷ 43

Rounding for one significant figure, we get

= 600 ÷ 40

= 15

So, the number of eggs in each basket is 15.

Problem 14 :

The month of December has 31 days. Estimate the number of seconds in December. Compare your estimate with correct value.

Solution :

Number of days in December = 31

Number of hours in one day = 24 hours.

1 hour = 60 minutes

1 minute = 60 seconds

To convert hour to seconds, we have to multiply by 3600.

Total number of seconds in December = 31 x 3600

= 111600 seconds ----(1)

Estimating the number of seconds :

Rounding to one significant figure, we get

= 30 x 4000

= 120000 seconds-----(2)

In (1), approximating the figure, we get 120000 seconds.