ESTIMATE THE DERIVATIVE OF A FUNCTION AT A GIVEN POINT FROM TABLE
To estimate the derivative of a function at a given point from table, we have to follow the steps given below.
Step 1 :
Determine the slope between point and the point directly to the left of point .
Step 2 :
Determine the slope between point and the point directly to the right of point.
Use the tables to estimate the value of the derivative at the given point. Indicate units of measures.
Problem 1 :
|
a. f'(8) |
b. f'(3.5) |
Solution :
a. To find f'(8) :
Here 8 lies between 7 and 9.
(7, 807) and (9, 902)
f'(8) = 47.5 visitors/hours
b. To find f'(3.5) :
f'(3.5) = 119 visitors/hours
Problem 2 :
|
a. f'(17) |
b. f'(24.5) |
Solution :
a. To find f'(17) :
f'(17) = -1.667 ºC per cm
b. To find f'(24.5) :
f'(24.5) = -3.667 ºC per cm
Problem 3 :
|
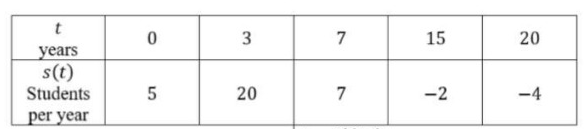
a. f'(1.5) |
b. f'(11) |
Solution :
a. To find f'(1.5) :
f'(1.5) = 5 students/year2
b. To find f'(11) :
f'(11) = -1.125 students/year2
Problem 4 :
|
a. f'(47.5) |
b. f'(9) |
Solution :
a. To find f'(47.5) :
f'(47.5) = 3 pages per day
b. To find f'(9) :
f'(9) = -3.875 pages per day
Problem 5 :
|
a. f'(20) |
b. f'(82.5) |
Solution :
a. To find f'(20) :
f'(20) = -10.75 gallons/sec2
b. To find f'(82.5) :
f'(82.5) = -6.4285 gallons/sec2
Problem 6 :
|
a. f'(25.5) |
b. f'(13.5) |
Solution :
a. To find f'(25.5) :
f'(25.5) = 13.555 yards per carry
b. To find f'(13.5) :
f'(13.5) = -3 yards per carry
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling