EQUATION PRACTICE WITH ANGLE ADDITION

To solve problems in this topic, we have to analyze the following.

Check the relationship between the angles involving.

Example 1 :

Find the value of x.

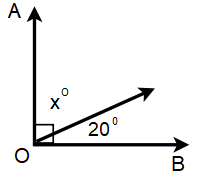
Solution :

By observing AOB, it is complementary. So, sum of the angles is 90.

x + 20 = 90

Subtracting 20 on both sides, we get

x = 90 - 20

x = 70

Example 2 :

Find x.

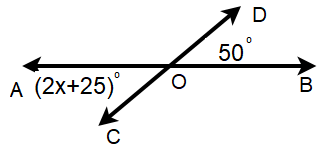
Solution :

∠AOC = ∠BOD (Vertically opposite angles)

2x + 25 = 50

Subtracting 25 on both sides, we get

2x = 50 - 25

2x = 25

Dividing by 2 on both sides.

x = 25/2

x = 12.5

Example 3 :

Find x.

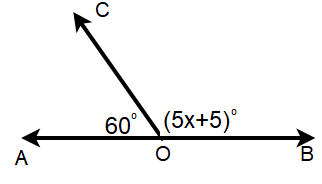
Solution :

AOB is a straight line. Its angle measure is 180.

∠AOC + ∠BOC = 180

60 + 5x + 5 = 180

5x + 65 = 180

Subtracting 65.

5x = 180 - 65

5x = 115

Divide by 5.

x = 115/5

x = 23

Example 4 :

Find x.

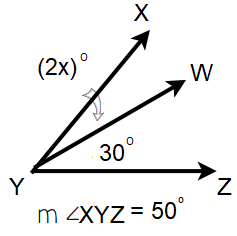
Solution :

∠XYZ = ∠XYW + ∠WYZ

50 = 2x + 30

Subtracting 30.

2x = 50 - 30

2x = 20

Dividing by 2.

x = 20/2

x = 10

Example 5 :

Find x.

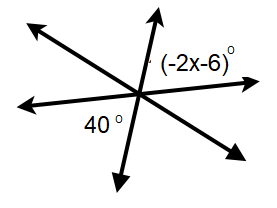
Solution :

By observing the picture given above, they are vertically opposite angles.

-2x - 6 = 40

Adding 6 on both sides.

-2x = 40 + 6

-2x = 46

Dividing by -2 on both sides.

x = 46/(-2)

x = -23

Example 6 :

Find the value of x.

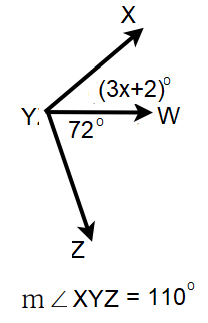
Solution :

∠XYW = 3x + 2

∠WYZ = 72

∠XYZ = 110

∠XYW + ∠WYZ = ∠XYZ

3x + 2 + 72 = 110

3x + 74 = 110

Subtracting 74 on both sides.

3x = 110 - 74

3x = 36

Dividing by 3 on both sides.

x = 36/3

x = 12

Example 7 :

Find the angle B.

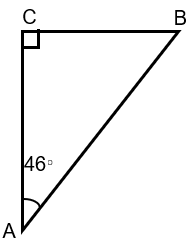
Solution :

In triangle ABC,

∠A + ∠B + ∠C = 180

Here ∠C = 90, ∠A = 46

46 + ∠B + 90 = 180

136 + ∠B = 180

∠B = 180 - 136

∠B = 44

Example 8 :

Find ∠JKX

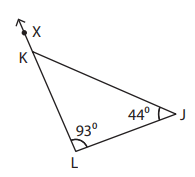
Solution :

Using exterior angle theorem.

∠JKX = ∠KLJ + ∠LJK

∠JKX = 93 + 44

∠JKX = 137

Example 9 :

Find the value of x.

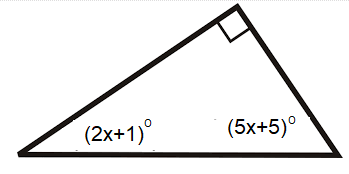
Solution :

In the triangle, the sum of interior angles is 180.

2x + 1 + 5x + 5 + 90 = 180

By combining the like terms, we get

7x + 96 = 180 

Subtracting 96 on both sides.

7x = 180 - 96

7x = 84

Dividing by 7 on both sides.

x = 84/7

x = 12

Example 10 :

Find the value of x and y.

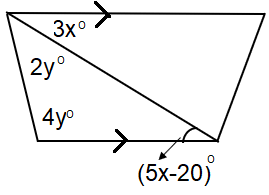
Solution :

From the picture, the opposite sides are parallel.

So, 3x and 5x-20 are alternate angles.

3x = 5x - 20

-2x = -20

x = 10

Sum of interior angle of triangle = 180

2y + 4y + 5x - 20 = 180

6y + 5x - 20 = 180

Add 20 on both sides.

6y + 5x = 180 + 20

6y + 5x = 200 -------(1)

Applying the value of x  in (1)

6y + 5(10) = 200

6y + 50 = 200

By subtracting 50 on both sides.

6y = 200 - 50

6y = 150

Dividing by 6 on both sides, we get

y = 150/6

y = 25