EQUATION OF HORIZONTAL ASYMPTOTE

Horizontal Asymptotes :

A horizontal asymptote is a horizontal line that is not part of a graph of a function but guides it for x – values “far” to the right and/or “far” to the left. The graph may cross it but eventually, for large enough or small enough values of x (approaching ±∞), the graph would get closer and closer to the asymptote without touching it.

A horizontal asymptote is a special case of a slant asymptote.

Let

deg N(x) = the degree of a numerator

and

deg D(x) = the degree of a denominator

Find the horizontal asymptote of the graph of each rational function.

Problem 1 :

y = 2/(x – 6)

Solution :

 y = 2/(x – 6)

Degree of numerator = 0

Degree of denominator = 1

degree of numerator < degree of denominator

So, equation of the horizontal asymptote is y = 0 which is the x – axis.

Problem 2 :

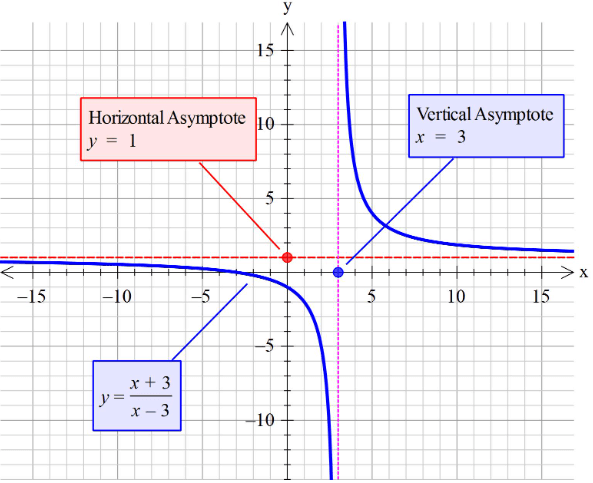
y = (x + 2)/(x – 4)

Solution :

y = (x + 2)/(x – 4)

Degree of numerator = 1

Degree of denominator = 1

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

So, equation of the horizontal asymptote is y = 1.

Problem 3 :

y = (x + 3)/2(x + 4)

Solution :

Given, y = (x + 3)/2(x + 4)

Degree of numerator = 1

Degree of denominator = 1

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

So, equation of the horizontal asymptote is y = 1/2.

Problem 4 :

y = (2x² + 3)/(x² – 6)

Solution :

y = (2x² + 3)/(x² – 6)

Degree of numerator = 2

Degree of denominator = 2

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

So, equation of the horizontal asymptote is y = 2.

Problem 5 :

y = (3x - 12)/(x² – 2)

Solution :

Given, y = (3x - 12)/(x² – 2)

Degree of numerator = 0

Degree of denominator = 2

degree of numerator < degree of denominator

So, equation of the horizontal asymptote is y = 0 which is the x – axis.

Problem 6 :

y = (3x³ – 4x + 2)/(2x³ + 3)

Solution :

y = (3x³ – 4x + 2)/(2x³ + 3)

Degree of numerator = 3

 Degree of denominator = 3

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

y = 3/2

So, equation of the horizontal asymptote is y = 1.5.