FIND THE EQUATION OF ELLIPSE FROM FOCI AND LENGTH OF MAJOR OR MINOR AXIS
In ellipse vertices, foci and center they lie in the same line and on the major axis.
- Midpoint of foci is center.
- Midpoint of vertices is center.
- Length of major axis is 2a
- Length of minor axis is 2b.
Problem 1 :
Foci: (±5, 0); major axis of length 12
Solution:
Foci are F1 (5, 0) and F2 (-5, 0). By observing the given foci, the ellipse is symmetric about x-axis.
Length of major axis = 12
2a = 12
a = 6
Midpoint of foci = center
Here the foci are on the x-axis, so the major axis is along the x-axis.
So, the equation of the ellipse is
2a = 12
a = 6
a2 = 36
c = 5
b2 = a2 - c2
b2 = 62 - 52
b2 = 36 - 25
b2 = 11
Hence the required equation of ellipse is
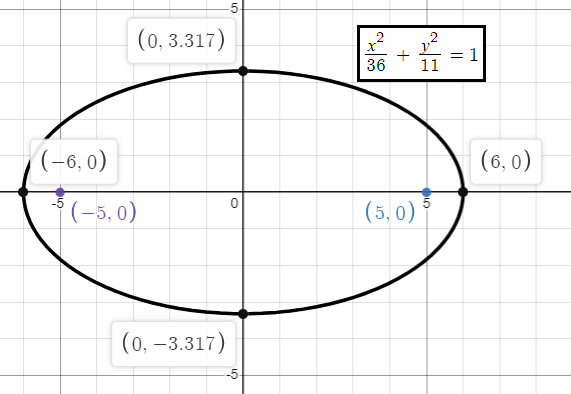
Problem 2 :
Foci: (±2, 0); major axis of length 8
Solution:
Given the major axis is 8 and foci are (±2, 0).
Here the foci are on the x-axis, so the major axis is along the x-axis.
So, the equation of the ellipse is
2a = 8
a = 4
a2 = 16
c = 2
b2 = a2 - c2
b2 = 42 - 22
b2 = 16 - 4
b2 = 12
Hence the required equation of ellipse is
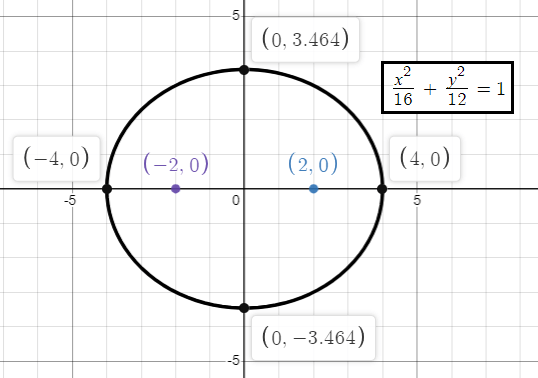
Problem 3 :
Foci: (0, 0), (4, 0); major axis of length 8
Solution:
The midpoint between the foci is the center
The distance between the foci is equal to 2c
The major axis length is equal to 2a
2a = 8
a = 4
b2 = a2 - c2
= 42 - 22
= 16 - 4
b2 = 12
The standard equation of an ellipse with a horizontal major axis is
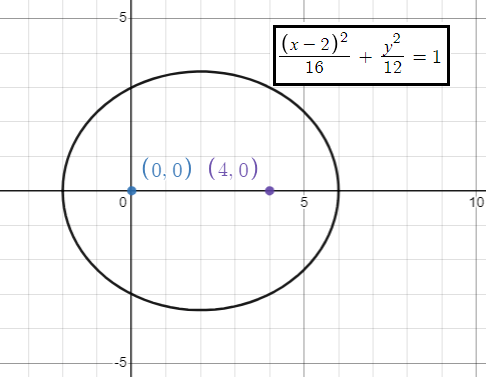
Problem 4 :
Foci: (0, 0), (0, 8); major axis of length 16
Solution:
The midpoint between the foci is the center
The distance between the foci is equal to 2c
The major axis length is equal to 2a
2a = 16
a = 8
b2 = a2 - c2
b2 = 82 - 42
b2 = 64 - 16
b2 = 48
By observing foci, since x-coordinates are same. The ellipse is symmetric about y-axis.
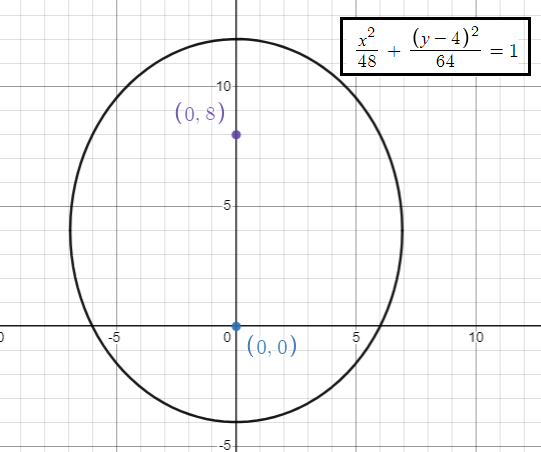
Problem 5 :
Vertices: (0, 4), (4, 4); minor axis of length 2
Solution:
The center of the ellipse
By observing center and foci, the ellipse is symmetric about x-axis.
Length of minor axis = 2
2b = 2
b = 1
Length of the major axis
a2 = 16
Equation of the ellipse
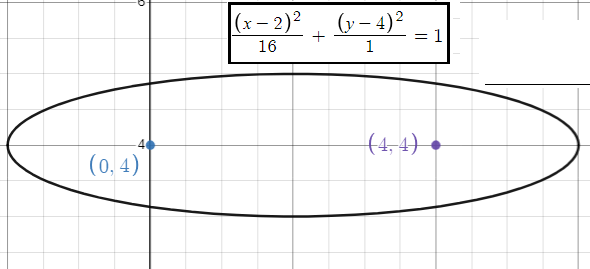
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling