EQUATION OF A TRANSLATED CIRCLE FROM STANDARD FORM

Problem 1 :

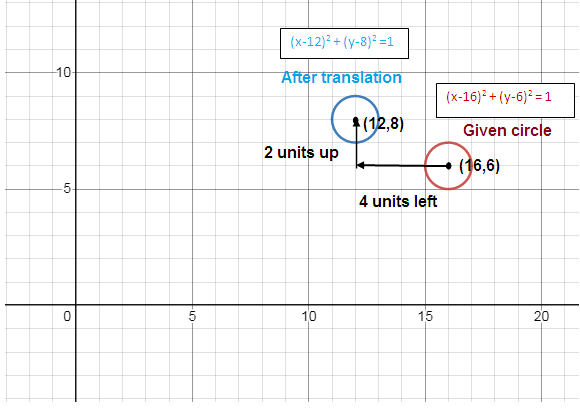
(x - 16)² + (y - 6)² = 1

Translated 4 left, 2 up

Solution:

The standard form of a circle is

(x - h)² + (y - k)² = r²

Where r is the radius of the circle and (h, k) is the center of the circle.

Center (h, k) = (16, 6)

When the circle is translated left 4 units and up 2 units.

The center should be changed as,

((x - 16) - (-4))² + ((y - 6) - (2))² = 1

(x - 16 + 4)² + (y - 6 - 2)² = 1

(x - 12)² + (y - 8)² = 1

Problem 2 :

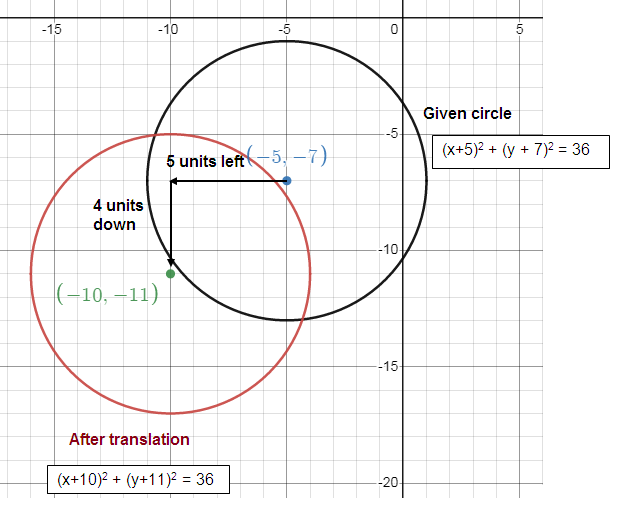
(x + 5)² + (y + 7)² = 36

Translated 5 left, 4 down

Solution:

The standard form of a circle is

(x - h)² + (y - k)² = r²

Where r is the radius of the circle and (h, k) is the center of the circle.

(x - (-5))² + (y - (-7))² = 36

Center (h, k) = (-5, -7)

Translating 5 units left and 4 units down

((x + 5) - (-5))² + ((y + 7) - (-4))² = 36

(x + 5 + 5)² + (y + 7 + 4)² = 36

(x + 10)² + (y + 11)² = 36

Problem 3 :

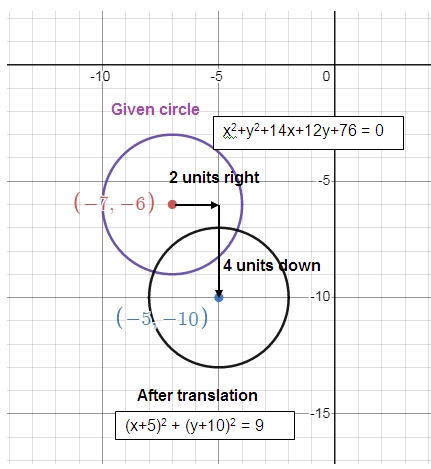
x² + y² + 14x + 12y + 76 = 0

Translated 2 right, 4 down

Solution:

x² + y² + 14x + 12y + 76 = 0

x² + 14x + y² + 12y + 76 = 0

x² + 2 ⋅ x ⋅ 7 + 7² - 7² + y² + 2 ⋅ y ⋅ 6 + 6² - 6² + 76 = 0

(x + 7)² - 49 + (y + 6)² - 36 + 76 = 0

(x + 7)² + (y + 6)² - 85 + 76 = 0

(x + 7)² + (y + 6)² = 9

Before translation :

Center of the circle is (7, -6).

(x + 7)² + (y + 6)² = 9

After translation :

(x + 7 - 2)² + (y + 6 - (-4))² = 9

Translated 2 right, 4 down

So, equation of new circle is,

(x + 5)² + (y + 10)² = 9

Problem 4 :

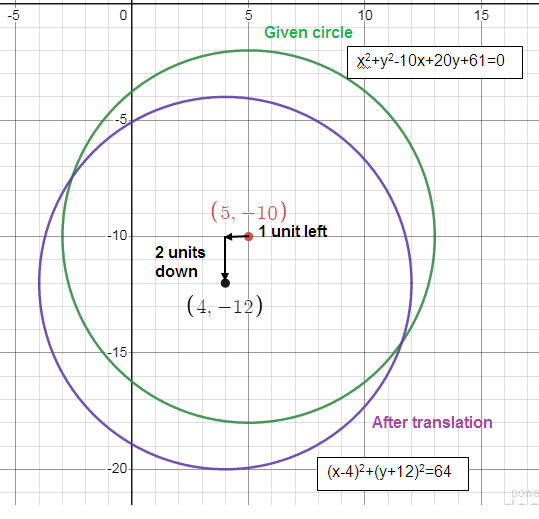
x² + y² - 10x + 20y + 61 = 0

Translated 1 left, 2 down

Solution:

x² + y² - 10x + 20y + 61 = 0

x²  - 2 ⋅ x ⋅ 5 + 5² - 5²+ y²+ 2 ⋅ y ⋅ 10 + 10² - 10² + 61 = 0

(x - 5)²  - 25 + (y + 10)² - 100 + 61 = 0

(x - 5)² + (y + 10)² - 25 - 100 + 61 = 0

(x - 5)² + (y + 10)² - 64 = 0

(x - 5)² + (y + 10)² = 64

Before translation, the center will be at :

(5, -10)

(x - 5)² + (y + 10)² = 64

After translation, the center will be at :

Translated 1 left, 2 down

(x - 5 - (-1))² + ((y + 10) - (-2))² = 64

(x - 5 + 1)² + (y + 10 + 2)² = 64

(x - 4)² + ((y + 12)² = 64

Problem 5 :

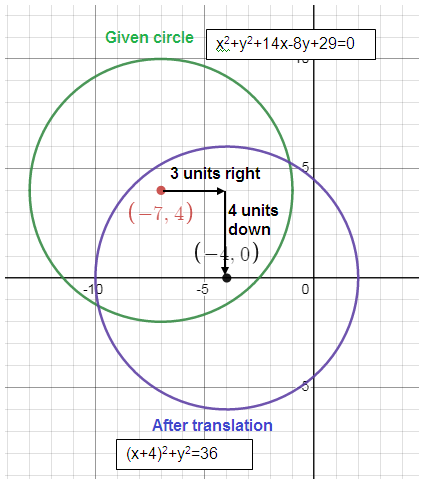
x² + y² + 14x - 8y + 29 = 0

Translated 3 right, 4 down

Solution:

x² + y² + 14x - 8y + 29 = 0

x² + 14x + y² - 8y + 29 = 0

x² + 2⋅x⋅7 + 7² - 7² + y² - 2⋅y⋅4 + 4²- 4² + 29 = 0

(x + 7)² - 49 + (y - 4)² - 16 + 29 = 0

(x + 7)² + (y - 4)² - 65 + 29 = 0

(x + 7)² + (y - 4)² - 36 = 0

(x + 7)² + (y - 4)² = 36

Before the translation, center will be at :

(-7, 4)

After the translation, center will be at :

(x + 7 - 3)² + (y - 4 - (-4))² = 36

(x + 4)² + (y - 4 + 4)² = 36

(x + 4)² + y² = 36

Problem 6 :

4y + y² = -28x - x² - 191

Translated 4 right

Solution:

4y + y² = -28x - x² - 191

x² + 28x + y² - 4y + 191 = 0

(x + 14)² + (y - 2)² - 14² - 2²+ 191 = 0

(x + 14)² + (y - 2)² - 196  - 4 + 191 = 0

(x + 14)² + (y - 2)² - 200 + 191 = 0

(x + 14)² + (y - 2)² - 9 = 0

(x + 14)² + (y - 2)²  = 9

Thus the coordinates of the center at (-14, -2). When the circle is translated right 4 units,

h = -14 + 4 = -10

So, equation of new circle is,

(x + 10)² + (y + 2)² = 9