DRAW THE GRAPH OF INVERSE FUNCTION FROM GIVEN GRAPH

Graph the inverse for each relation below (put your answer on the same graph).

Problem 1 :

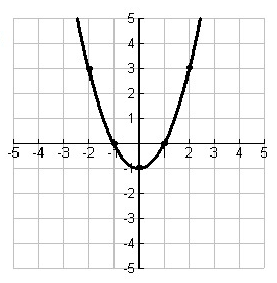
Solution:

By observing the points from the graph of f(x),

(-2, -3) (-1, 0) (0, -1) (1, 0) and (2, 3)

Representing it as table,

Inverse function:

Let f^-1(x) be the inverse of the given function f(x). To get the points on the graph of inverse function, we have to exchange the values of x and y.

Points to the plotted to make inverse function.

Points on Inverse graph :

(-3, -2) (0, -1) (-1, 0) (0, 1) and (3, 2)

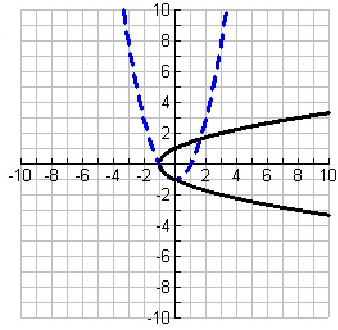
Problem 2 :

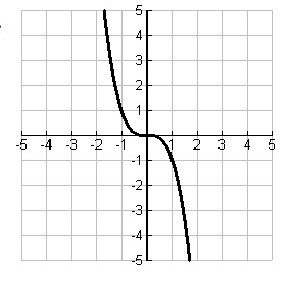
Solution:

By observing the points from the graph of f(x),

(-1, 1) (0, 0) and (1, -1)

Representing it as table,

Inverse function:

Let f^-1(x) be the inverse of the given function f(x). To get the points on the graph of inverse function, we have to exchange the values of x and y.

(1, -1) (0, 0) and (-1, 1)

Problem 3 :

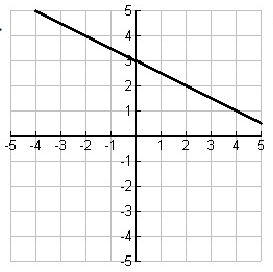
Solution:

By observing the graph, we get the points

Points of f(x) :

(-2, 4) (0, 3) (2, 2) (4, 1)

Points to be plotted on f^-1(x) :

(4, -2) (3, 0) (2, 2) (1, 4)

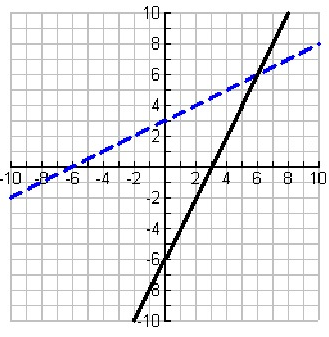
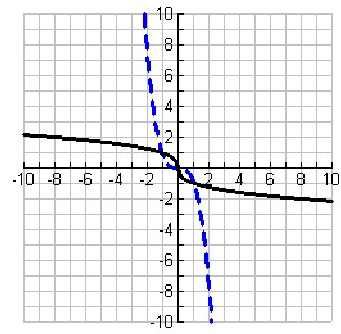
Problem 4 :

Solution:

Points of f(x) :

By observing the points from the graph of f(x),

 (0, 0) (1, 1) and (4, 2)

Representing it as table,

Inverse function:

Let f^-1(x) be the inverse of the given function f(x). To get the points on the graph of inverse function, we have to exchange the values of x and y.

(0, 0) (1, 1) and (2, 4)

Problem 5 :

a. Use the graph of the function to complete the table for f^-1.

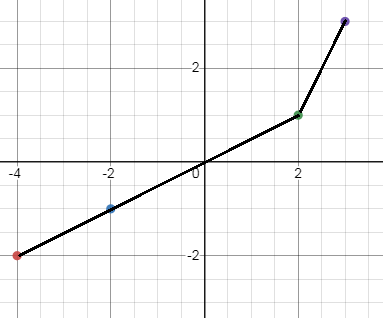
b. Then use the table to sketch f^-1.

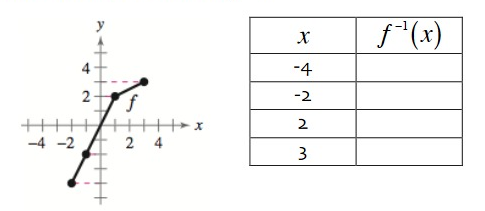
Solution:

a.

Points of f(x) :

By observing the points from the graph of f(x),

 (-2, -4) (-1, -2) (1, 2) and (3, 3)

Representing it as table,

Points to be plotted on f^-1(x) :

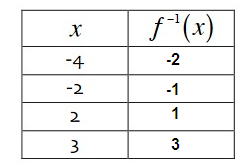
b.

Problem 6 :

Use the graphs of f and g to evaluate each expression.

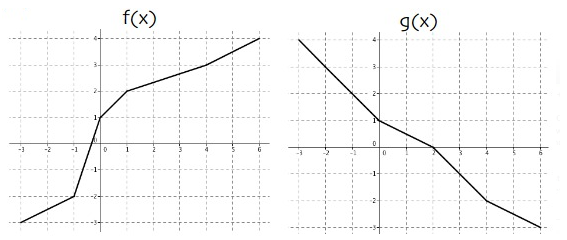
1. f^-1(1)

2. (g^-1)(0)

3. (f ∘ g)(0)

4. g(f(4))

5. (f^-1 ∘ g)(0)

6. (g^-1 ∘ f)(-1)

7. (f ∘ g^-1)(2)

8. (f^-1 ∘ g^-1)(-2)

Solution:

f(x) :

g(x):

1. 

f^-1(1) = 0

2. 

(g^-1)(0) = 2

3.

(f ∘ g)(0) = f(g(0))

= f(1)

= 2

4.

g(f(4)) = g(3)

= -1

5.

(f^-1 ∘ g)(0) = f^-1(g(0))

= f^-1(1)

= 0

6.

(g^-1 ∘ f)(-1) = g^-1(f(-1))

= g^-1(-2)

= 4

7.

(f ∘ g^-1)(2) = f(g^-1(2))

= f(-1)

= -2

8.

(f^-1 ∘ g^-1)(-2) = f^-1(g^-1(-2))

= f^-1(4)

= 6

Problem 7 :

1. If the composite functions f(g(x)) = x and g(f(x)) = x then the function g is the ________ function of f.

2. The domain of f is the ________ of f^-1 and the ________ of f^-1 is the range of f.

3. The graphs of f and f^-1 are reflections of each other in the line ________.

4. A function f is ________ if each value of the dependent variable corresponds to exactly one value of the independent variable.

5. A graphical test for the existence of an inverse function of is called the _______ Line Test.

Solution :

1) If f ∘ g (x) = g ∘ f(x), then f and g a re inverse to each other.

2) The domain of f is range of f^-1 and range of f is domain of f^-1.

3)  The graphs of f and f^-1 reflection of y = x.

4) one to one

5)  The horizontal line test is used to check if the function is one to one.

Problem 8 :

Match the graph of the function with the graph of its inverse function. [The graphs of the inverse functions are labeled (a), (b), (c), and (d).]

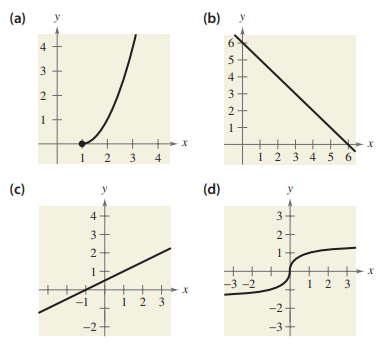
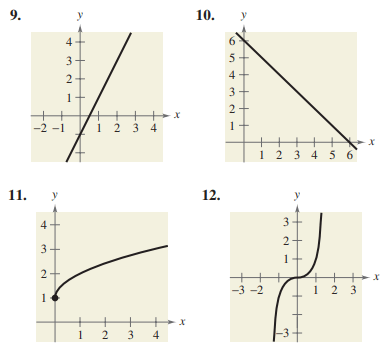
Solution :

Question a :

Some of the point in the graph a :

(1, 0) (2, 1) (3, 4)

Points on inverse function (0, 1) (1, 2) (4, 3)

Question b :

Some of the point in the graph b :

(1, 5) (2, 4) (3, 3) (6, 0) and (0, 6)

Points on inverse function (5, 1) (4, 2) (3, 3) (0, 6) (6, 0)

Question c :

Some of the point in the graph c :

(1, 1) (-1, 0) (3, 2)

Points on inverse function (1, 1) (0, -1) (2, 3)

Question d :

Some of the point in the graph d :

(1, 1) (0, 0) (-1, -1)

Points on inverse function (1, 1) (0, 0) (-1, -1)

Answers :

Question a ==> 11

Question b ==> 10

Question c ==> 9

Question d ==> 12