DOUBLE ANGLE FORMULA IN TRIGONOMETRY

Double Angle Formulae

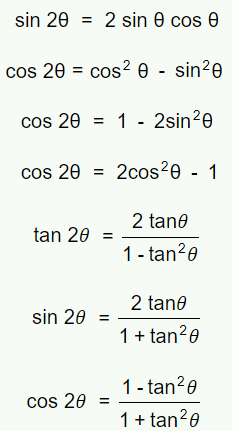
Use an appropriate 'double angle' formula to simplify:

Problem 1 :

2 sin α cos α

Solution:

= 2 sin α cos α

= sin 2α

Problem 2 :

4 cos α sin α

Solution:

= 4 cos α sin α

= 2 × 2 cos α sin α

= 2 sin 2α

Problem 3 :

sin α cos α

Solution:

= sin α cos α

Multiplying and dividing by 2, we get

= (2/2) sin α cos α

= (1/2) (2sin α cos α)

= (sin 2α/2)

Problem 4 :

2 cos² β - 1

Solution:

= 2 cos² β - 1

= cos 2β 

Problem 5 :

1 - 2 cos² ϕ

Solution:

= 1 - 2 cos² ϕ

= - (2 cos² ϕ - 1)

= - cos 2ϕ

Problem 6 :

1 - 2 sin² N

Solution:

= 1 - 2 sin² N

= cos 2N

Problem 7 :

2 sin² M - 1

Solution:

= 2 sin² M - 1

= - (1 - 2 sin² M)

= - cos 2M

Problem 8:

cos² α - sin² α

Solution:

= cos² α - sin² α

= cos 2α

Problem 9 :

sin² α - cos² α

Solution:

= sin² α - cos² α

= - (cos² α - sin² α)

= - cos 2α

Problem 10 :

2 sin 2A cos 2A

Solution:

= 2 sin 2A cos 2A

= sin (2 × 2A)

= sin 4A

Problem 11 :

2 cos 3α sin 3α

Solution:

= 2 cos 3α sin 3α

= sin (2 × 3α)

= sin 6α

Problem 12 :

2 cos² 4θ - 1

Solution:

= 2 cos² 4θ - 1

It is in the form of 2 cos² θ - 1, instead of θ we have 4θ

= cos (2 × 4θ)

= cos 8θ

Problem 13 : 

1 - 2 cos² 3β

Solution :

= 1 - 2 cos² 3β

= - (2 cos² 3β - 1)

= - cos (2 × 3β)

= - cos 6β

Problem 14 :

1 - 2 sin² 5α

Solution:

= 1 - 2 sin² 5α

= cos (2 × 5α)

= cos 10α

Problem 15 :

2 sin² 3D - 1

Solution:

= 2 sin² 3D - 1

= - (1 - 2 sin² 3D)

= - cos (2 × 3D)

= - cos 6D

Problem 16 :

cos² 2A - sin² 2A

Solution:

= cos² 2A - sin² 2A

The given question looks like cos² A - sin² A, Here A = 2A

cos² A - sin² A = cos 2A

cos² 2A - sin² 2A = cos 2(2A)

= cos 4A

Problem 17 :

cos² (α/2) - sin² (α/2)

Solution:

= cos² (α/2) - sin² (α/2)

The given question looks like cos² A - sin² A, Here A = α/2

cos² A - sin² A = cos 2A

= cos (2 × α/2)

= cos α

Problem 18 :

2 sin² 3P - 2 cos² 3P

Solution:

= 2 sin² 3P - 2 cos² 3P

Factoring 2

= 2(sin² 3P - cos² 3P)

= -2(cos² 3P - sin² 3P)

= 2(cos(2 × 3P))

= - 2 cos (2 × 3P)

= -2 cos 6P