DOMAIN OF TANGENT FUNCTION AND INVERSE TANGENT FUNCTION
Properties of the tangent function :
From the graph of y = tan x, we observe the following properties of tangent function.
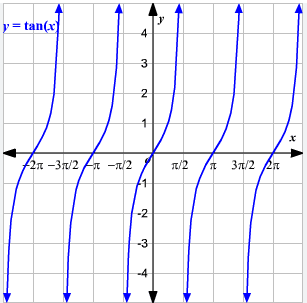
i) The graph is not continuous and has discontinuity points at
ii) The partial graph is symmetric about the origin for
iii) It has infinitely many vertical asymptotes x
n belongs to Z
iv) The tangent function has neither maximum not minimum.
Properties of inverse tangent function :
For any real number x, define tan-1x as the unique number y in (-π/2, π/2) such that tan y = x.
i) y = tan-1x, if and only if x = tan y for x ∈ R and -π/2 < y < π/2
ii) tan (tan-1x) = x for any real number x and y = tan-1x is an odd function.
iii) tan-1(tan x) = x, if and only if -π/2 < y < π/2
Find the domain of the following function
Problem 1 :
tan-1 (√(9 - x2))
Solution :
Range of tangent function will be the domain of tangent inverse function.
- ∞ ≤ tan-1 x ≤ ∞
Domain of tan-1 x will be all real values.
√(9 - x2) ≥ 0
Take square on both sides
(9 - x2) ≥ 0
-x2 ≥ -9
x2 ≤ 9
x ≤ ±3
Decomposing into intervals, we get
(- ∞, -3] [-3, 3] and [3, ∞)
|
x = -4 ∈(- ∞, -3] (9 - (-4)2) ≥ 0 (9 -16) ≥ 0 -7 ≥ 0 (False) |
x = 0 ∈ [-3, 3] (9 - 02) ≥ 0 9 ≥ 0 9 ≥ 0 (True) |
x = 4 ∈ [3, ∞) (9 - 42) ≥ 0 -7 ≥ 0 -7 ≥ 0 (False) |
So, domain for the function tan-1 (√(9 - x2)) is [-3, 3].
Problem 2 :
Solution :
Domain of tan-1 x will be all real values. Like a previous problem, we have 1 - x2. Even getting negative values is also not a problem. So, all real values will be domain.
Find the value of the following.
Problem 3 :
Solution :
Problem 4 :
Solution :
Problem 5 :
Solution :
Here 7π/4 is output for tangent function. It is acceptable. Because for tangent function, the output may be all real values.
Problem 6 :
Solution :
Problem 7 :
Solution :
Problem 8 :
Solution :
Find the value of
Problem 9 :
Solution :
cos-1 (1/2) :
For what angle measure of cosine, we get 1/2 as output.
cos-1 (1/2) = π/3
sin-1(-1/2) :
For what angle measure of cosine, we get 1/2 as output.
sin(π - π/6) = sin(5π/6)
sin(π - π/6) = sin(-π/6) ==> -sin(π/6) = -1/2
-π/6 ∈ [-π/2, π/2]
sin-1(-1/2) = -π/6
Problem 10 :
Solution :
Problem 11 :
Solution :
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling