DOMAIN OF COMPOSITION OF FUNCTIONS

For each of the following problems :

(a)  Find f ∘ g and its domain.

(b) Find g ∘ f and its domain. 

Problem 1 :

f(x) = x² + 3x; g(x) = 2x - 7

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

= f[2x - 7]

= (2x - 7)² + 3(2x - 7)

= (2x)² + 7² - 2(2x)(7) + 6x - 21

= 4x² + 49 - 28x + 6x - 21

(f ∘ g)(x) = 4x² - 22x + 28

Domain is all real values of x.

So, domain of f ∘ g is (-∞, ∞).

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

= g[x² + 3x]

= 2(x² + 3x) - 7

(g ∘ f)(x) = 2x² + 6x - 7

Domain is all real values of x.

So, domain of g ∘ f is (-∞, ∞).

Problem 2 :

f(x) = 6x + 2; g(x) = 7 - x²

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

= f[7 - x²]

= 6(7 - x²) + 2

= 42 - 6x² + 2

(f ∘ g)(x) = 44 - 6x²

So, domain of f ∘ g is (-∞, ∞).

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

= g[6x + 2]

= 7 - (6x + 2)²

= 7 - [(6x)² + 2² + 2(6x)(2)]

= 7 - [36x² + 4  + 24x] 

= 7 - 36x² - 4 - 24x

(g ∘ f)(x) = -36x² - 24x  + 3

So, domain of g ∘ f is (-∞, ∞).

Problem 3 :

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

So, domain of f ∘ g is all real numbers expect 4.

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

= g(x²)

√(x² - 4) ≥ 0

(x² - 4) ≥ 0

(x + 2)(x - 2) ≥ 0

By drawing number line, we will get the solution more clearly.

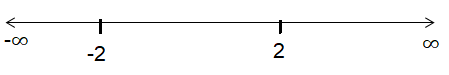
x = -3 ∈ (-∞, -2)

Appling the above value in (x + 2) (x - 2) ≥ 0, we get

(-3+2)(-3-2) ≥ 0

True

x = 0 ∈ (-2, 2)

Appling the above value in (x + 2) (x - 2) ≥ 0, we get

(0+2)(0-2) ≥ 0

False

x = 4 ∈ (2, ∞)

Appling the above value in (x + 2) (x - 2) ≥ 0, we get

(4+2)(4-2) ≥ 0

True

So, domain of g ∘ f is (-∞, -2) ∪ (2, ∞).

Problem 4 :

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

= f(x)²

Domain is all real values. Because no values will make the denominator as zero. Then the entire function will not become undefined for any values.

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

So, domain of g ∘ f is all real numbers except -5.

Problem 5 :

f(x) = √(x + 7); g(x) = -5 - x

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

= f[-5 - x]

= √(-5 - x + 7)

(f ∘ g)(x) = √(2 - x)

So, domain of f ∘ g is  (-∞, 2]

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

= g[√(x + 7)]

(g ∘ f)(x) = -5 - √(x + 7)

So, domain of g ∘ f is  [-7, ∞).

Problem 6 :

f(x) = √(3 - x); g(x) = 9 - 2x

Solution :

(a) To find f ∘ g and its domain :

f ∘ g = f[g(x)]

= f[9 - 2x]

= √(3 - (9 - 2x))

= √(3 - 9 + 2x)

(f ∘ g)(x) = √(2x - 6)

So, domain of f ∘ g is [3, ∞).

(b) To find g ∘ f and its domain :

g ∘ f = g[f(x)]

= g[√(3 - x)]

= 9 - 2(√(3 - x))

(g ∘ f)(x) = 9 - 2√3 + 2x

So, domain of g ∘ f is (-∞, ∞).