DOMAIN AND RANGE OF EXPONENTIAL FUNCTIONS PRACTICE

Graph each function. Label two points.

Problem 1 :

f(x) = 2^x + 2

Domain:     Range:

Parent function and transformation:

Solution:

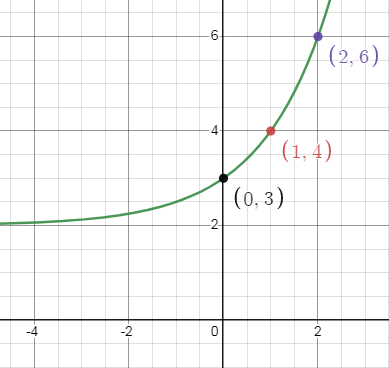
f(x) = 2^x + 2

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

Equation of horizontal asymptote is y = 2.

The range is y > 2.

Parent function:

y = a(b)^x

 f(x) = 2^x 

Transformation:

Horizontal shift: No shift

Vertical shift: 2 units up

Problem 2 :

f(x) = 3^x-1 

Domain:     Range:

Parent function and transformation:

Solution:

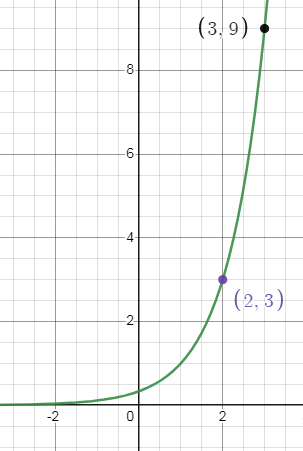
f(x) = 3^x-1 

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > 0.

Parent function:

y = a(b)^x

 f(x) = 3^x

Transformation:

Horizontal shift: Right 1 unit

Vertical shift: No shift

Problem 3 :

f(x) = 2^x-2 - 1 

Domain:     Range:

Parent function and transformation:

Solution:

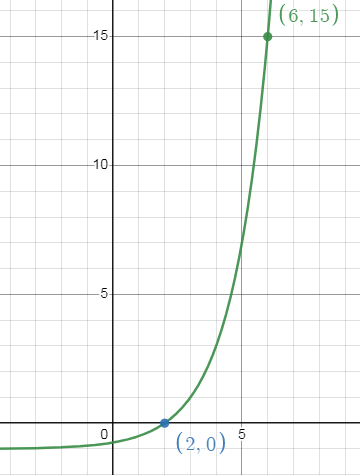
f(x) = 2^x-2 - 1 

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

Equation of horizontal asymptote is y = -1, since it is exponential growth function, the range is y > -1.

Parent function:

y = a(b)^x

 f(x) = 2^x

Transformation:

Horizontal shift: Right 2 units

Vertical shift: Down 1 unit

Problem 4 :

f(x) = -2^x+1 - 3

Domain:     Range:

Parent function and transformation:

Solution:

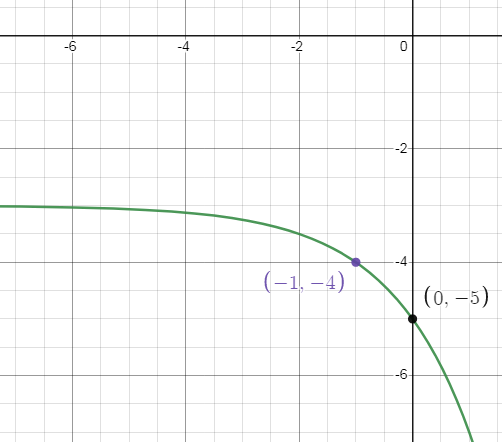
f(x) = -2^x+1 - 3

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

Equation of horizontal asymptote is y = -3, since it is exponential growth function but there is reflection across x-axis and the range is y < -3.

Parent function:

y = a(b)^x

 f(x) = 2^x

Transformation:

Horizontal shift: left 1 unit

Vertical shift: down 3 units

Problem 5 :

f(x) = -(3^x+1) + 2

Domain:     Range:

Parent function and transformation:

Solution:

f(x) = -(3^x+1) + 2

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

There is a reflection across x-axis, moving horizontally 1 unit to the left and moving up 2 units.

The range is y < 2.

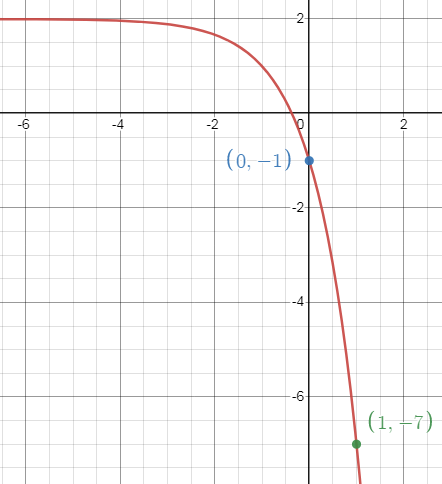
Parent function:

y = a(b)^x

 f(x) = 3^x

Transformation:

Horizontal shift: left 1 unit

Vertical shift: up 2 units

Problem 6 :

Domain:     Range:

Parent function and transformation:

Solution:

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > -3.

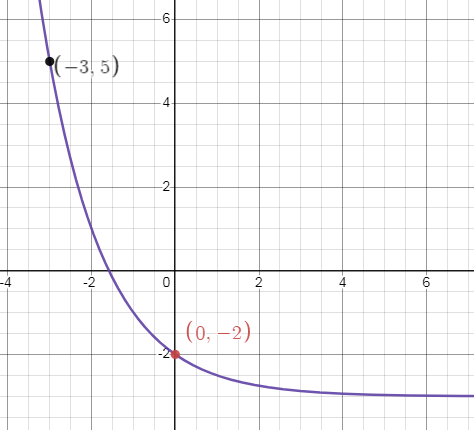
Parent function:

y = a(b)^x

 f(x) = 1/2^x

Transformation:

Horizontal shift: No shift

Vertical shift: Down 3 units

Problem 7 :

Domain:     Range:

Parent function and transformation:

Solution:

Domain:

Domain is the defined value of x. For this function, the domain is all real numbers.

Range:

The range is y > 1.

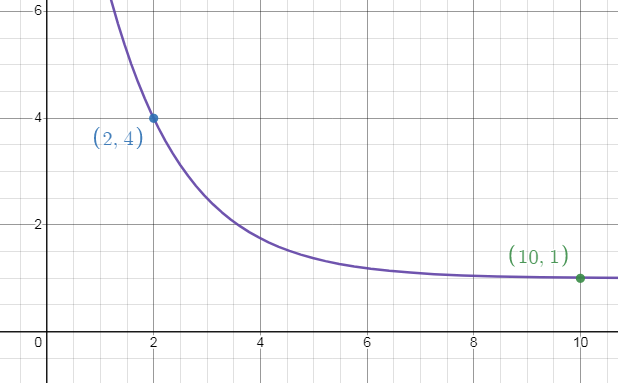
Parent function:

y = a(b)^x

 f(x) = 1/2^x

Transformation:

Horizontal shift: No shift

Vertical shift: Up 1 unit