DIVIDING POLYNOMIALS USING SYNTHETIC DIVISION

Use synthetic division to divide the polynomials given below, then find the quotient and remainder.

Problem 1 :

(x² + 8x + 1) ÷ (x - 4)

Solution :

Arrange dividend and the divisor in standard form.

Then,

x² + 8x + 1 (standard form of dividend)

x - 4 (standard form of divisor)

Find out the zero of the divisor.

x - 4 = 0

x = 4

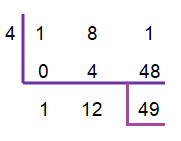
Therefore, the quotient is x + 12

And the remainder is 49.

Problem 2 :

(4x² - 13x - 5) ÷ (x - 2)

Solution :

Find out the zero of the divisor.

x - 2 = 0

x = 2

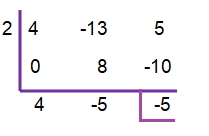
Therefore, the quotient is 4x - 5

And the remainder is -5

Problem 3 :

(2x² - x + 7) ÷ (x + 5)

Solution :

Find out the zero of the divisor.

x + 5 = 0

x = - 5

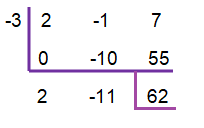
Therefore, the quotient is 2x - 11

And the remainder is 62.

Problem 4 :

(x³ - 4x + 6) ÷ (x + 3)

Solution :

Find out the zero of the divisor.

x + 3 = 0

x = -3

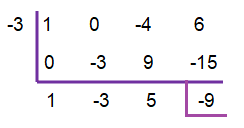
Therefore, the quotient is x² - 3x + 5

And the remainder is -9

Problem 5 :

(x² + 9) ÷ (x - 3)

Solution :

Find out the zero of the divisor.

x – 3 = 0

x = 3

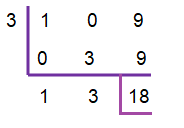
Therefore, the quotient is x + 3

And the remainder is 18

Problem 6 :

(3x³ - 5x² - 2) ÷ (x - 1)

Solution :

Find out the zero of the divisor.

x - 1 = 0

x = 1

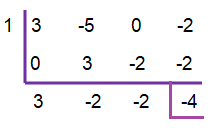
Therefore, the quotient is 3x² - 2x - 2

And the remainder is -4

Problem 7 :

(x⁴ – 5x³ - 8x² + 13x - 12) ÷ (x - 6)

Solution:

Find out the zero of the divisor.

x – 6 = 0

x = 6

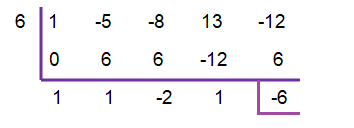
Therefore, the quotient is x³ + x² - 2x + 1

And the remainder is -6

Problem 8 :

(x⁴ + 4x³ + 16x - 35) ÷ (x + 5)

Solution :

Find out the zero of the divisor.

x + 5 = 0

x = -5

Therefore, the quotient is x³ - x² + 5x - 9

And the remainder is 10.

Problem 9 :

Describe and correct the error in using synthetic division to divide x³ − 5x + 3 by x − 2.

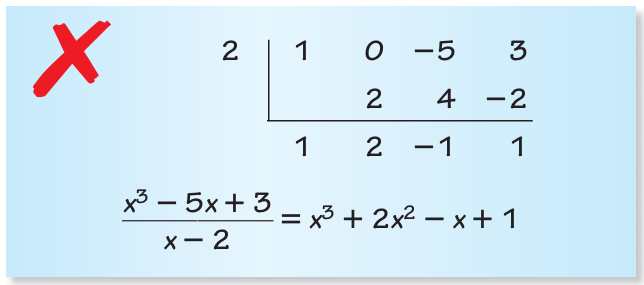
Solution :

There is no error in division part, since we are not getting 0 as remainder, the given polynomial x³ − 5x + 3 is not divisible by x - 2. Then, it should be written as 

(x³ − 5x + 3)/(x - 2) = x³ + 2x² - x + 1

It should be written as 

(x³ − 5x + 3)/(x - 2) = (x² + 2x - 1) + 1/(x - 2)

Problem 10 :

Describe and correct the error in using synthetic division to divide x³ − 5x + 3 by x − 2.

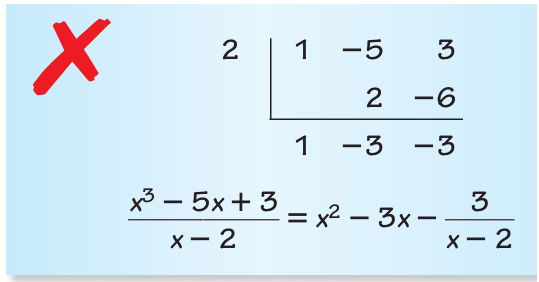
Solution :

By writting the polynomial in standard form, we get

x³ − 5x + 3

While dividing the polynomial using the method of long division or synthetic division, the missing term should be replaced as 0.

Problem 11 :

Jordan divided the polynomial x⁴ + x - 6 in to the polynomial p(x) yesterday. Today his work is smudged and he cannot read p(x) or most his answer. The only part he could read was the remainder x + 4. His teacher wants him to find p(-3), what is p(-3) ?

Solution :

The reamainder = x + 4

When x = -3

p(-3) = -3+ 4

= 1

So, the remainder is 1.

Problem 12 :

The volume V of the rectangular prism is given by V = 2x³ + 17x² + 46x + 40. Find an expression for the missing dimension.

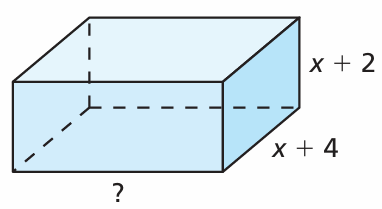
Solution :

V = 2x³ + 17x² + 46x + 40

Length = ?

Width = x + 4

Height = x + 2

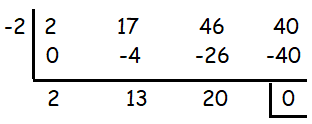
Quotient = 2x² + 13x + 20

= 2x² + 8x + 5x + 20

= 2x(x + 4) + 5(x + 4)

= (2x + 5)(x + 4)

Here the missing factor is 2x + 5. So, the length of the rectangular prism is 2x + 5.

Problem 13 :

You divide two polynomials and obtain the result

(5x² − 13x + 47) − [102/(x + 2)]

What is the dividend? How did you find it.

Solution :

(5x² − 13x + 47) − [102/(x + 2)]

= [(5x² − 13x + 47)(x + 2) - 102] / (x + 2)

= [(5x³ − 13x² + 47x + 10x² − 26x + 94) - 102] / (x + 2)

= [5x³ − 3x² + 21x + 94 - 102] / (x + 2)

= [5x³ − 3x² + 21x - 8] / (x + 2)

So, the dividend is 5x³ − 3x² + 21x - 8.

Problem 14 :

What is the value of k such that 

(-x⁴ + 5x² + kx - 8) ÷ (x - 4)

has a remainder of 0?

Solution :

Let p(x) = -x⁴ + 5x² + kx - 8

x - 4 = 0

x = 4

Apply x as 4

p(4) = -4⁴ + 5(4)² + k(4) - 8

= -256 + 5(16) + 4k - 8

0 = -256 + 80 + 4k - 8

0 = -184 + 4k

4k = 184

k = 184/4

= 46

So, the value of k is 46.