DIVIDING POLYNOMIALS BY TRINOMIALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Consider two polynomials f(x) and g(x), if we divide f(x) by g(x), we have to follow the given instruction.
Problem 1 :
(5x6 – 16x5 – 11x4 + 22x3 + 14x2 – 4x + 9) ÷ (x2 - 4x + 2)
Solution :
Let f(x) = 5x6 – 16x5 – 11x4 + 22x3 + 14x2 – 4x + 9
and
g(x) = x2 - 4x + 2
Step 1 :
Divide 5x6 by x2, so 5x6/x2 ==> 5x4
Put 5x4 at the top. Now, multiply 5x4 by (x2 - 4x + 2)
5x4 (x2 - 4x + 2) = 5x6 - 20x5 + 10x4
Write 5x6 - 20x5 + 10x4 below the given polynomial and then subtract.
Step 2 :
After subtraction, we will have a polynomial, take the first term from inside.
Here 4x5 should be divided by x2
4x5/x2 ==> 4x3
Now, multiply 4x3 by (x2 - 4x + 2)
4x3 (x2 - 4x + 2) = 4x5 - 16x4 + 8x3
Subtract this polynomial from the previous one.
Repeat the process until, we receive degree of the remainder be lesser than to degree of dividend.

Note :
If the order of the given polynomial is rearranged, then write it in the correct order and start division.
IF any term is missing replace it by 0 and then divide.
Problem 1 :
(6x4 – 30x2 + 24) ÷ (2x2 – 8)
Solution :
(6x4 – 30x2 + 24) ÷ (2x2 – 8)
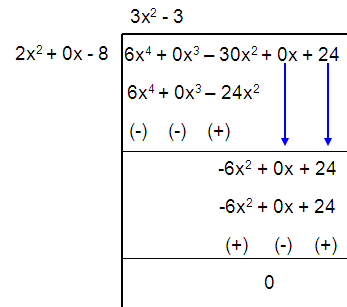
Quotient = 3x2 – 3
Remainder = 0
Problem 2 :
(3x5 + 4x3 – 5x + 8) ÷ (x2 + 3)
Solution :
(3x5 + 4x3 – 5x + 8) ÷ (x2 + 3)
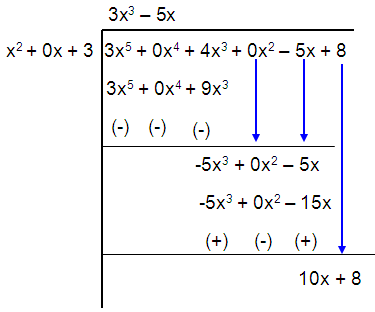
Quotient = 3x3 – 5x
Remainder = 10x + 8
Problem 3 :
(x5 + 2x4 + x3 – x2 – 22x + 15) ÷ (x2 + 2x – 3)
Solution :
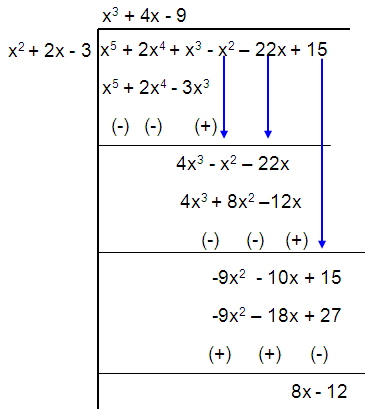
Quotient = x3 + 4x - 9
Remainder = 8x - 12
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling