DIVIDING POLYNOMIALS BY MONOMIALS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To divide a polynomial by a monomial, we can decompose the fraction into many fractions. Using the operations on exponents, we can simplify further.
Problem 1 :
Problem 2 :
Problem 3 :
Problem 4 :
Problem 5 :
Problem 6 :
Problem 7 :
Problem 8 :
Problem 9 :
Problem 10 :
Problem 11 :
Problem 12 :
Problem 13 :
Problem 14 :
Problem 15 :
Problem 16 :
Problem 17 :
Answer Key
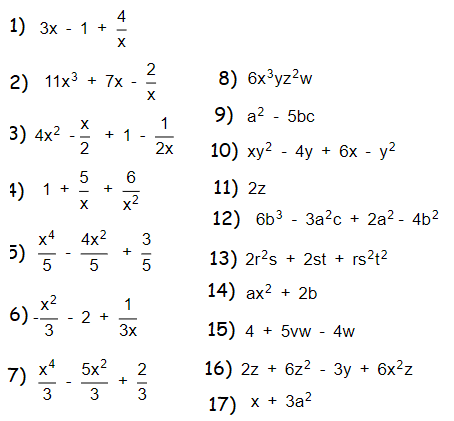
Divide. Write your answer in fraction form.
Problem 1 :
(2x5 – 15x3 – 9x2 + 11x + 12) ÷ (x + 2)
Problem 2 :
(x4 – x3 – 19x2 - 3x - 19) ÷ (x - 5)
Problem 3 :
(10x4 – 4x3 + 14x2 - 14x - 16) ÷ (2x - 2)
Problem 4 :
(9x5 – 9x4 – x3 - 12x2 + x - 11) ÷ (3x - 5)
Problem 5 :
(16x4 + 4x3 + 2x2 - 21x + 7) ÷ (4x - 1)
Problem 6 :
(6x5 + 21x4 – 14x3 - 8x2 + x - 6) ÷ (x + 4)
Answer Key
1) Quotient = 2x4 – 4x3 – 7x2 + 5x + 1
Remainder = 10
2) Quotient = x3 + 4x2 + x + 2
Remainder = -9
3) Quotient = 5x3 + 3x2 + 10x + 3
Remainder = -5
4) Quotient = 3x4 + 2x3 + 3x2 + x + 2
Remainder = -1
5) Quotient = 4x3 + 2x2 + x - 5
Remainder = 2
6) Quotient = 6x4 - 3x3 - 2x2 + 0x + 1
Remainder = -10
Answers in Fractional Form
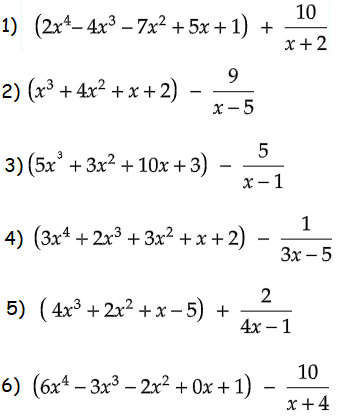
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling