DETERMINING IF THE SET OF POINTS WILL BE A PARALLELOGRAM

Problem 1 :

Verify that the quadrilateral with vertices P(-2, 2), Q(-2, -3), R(-5, -5) and S(-5, 0) is a parallelogram.

Solution :

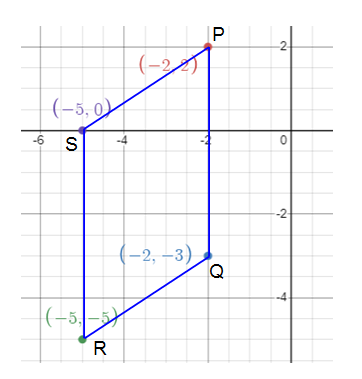
Slope of PQ :

P(-2, 2) and Q(-2, -3)

x₁ = -2, y₁ = 2, x₂ = -2, y₂ = -3

Slope of QR :

Q(-2, -3) and  R(-5, -5)

x₁ = -2, y₁ = -3, x₂ = -5, y2 = -5

Slope of RS :

R(-5, -5) and S(-5, 0)

x₁ = -5, y₁ = -5, x₂ = -5, y₂ = 0

Slope of SP :

S(-5, 0) and P(-2, 2)

x₁ = -5, y₁ = 0, x₂ = -2, y₂ = 2

The opposite sides PQ, RS and QR, SP have the same slope and are thus parallel to each other.

Midpoint of the diagonals :

Midpoint of diagonal PR :

P(-2, 2) and R(-5, -5)

Midpoint of S(-5, 0) and Q(-2, -3) :

Since the midpoints of the diagonal are equal and opposite sides are equal, it must be a parallelogram.

Problem 2 :

A quadrilateral has vertices K(-1, 4), L(2, 2), M(0, -1) and N(-3, 1). Verify that :

a) The quadrilateral is a square.

b) Each diagonal of the quadrilateral is the perpendicular bisector of the other diagonal.

c) The diagonals are equal in length.

Solution :

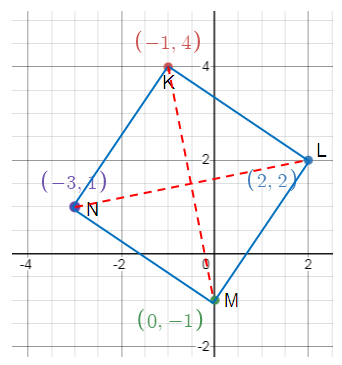
a)  Given, K(-1, 4), L(2, 2), M(0, -1) and N(-3, 1)

Length of  KL :

K(-1, 4) and L(2, 2)

x₁ = -5, y₁ = 0, x₂ = -2, y₂ = 2

KL = √[(-2 + 5)² + (2 - 0)²]

= √[(3)² + (2)²]

 = √[9 + 4]

KL = √13

Length of  LM : 

L(2, 2) and M(0, -1)

x₁ = 2, y₁ = 2, x₂ = 0 , y₂ = -1

LM = √[(0 - 2)² + (-1 - 2)²]

= √[(-2)² + (-3)²]

 = √[4 + 9]

LM = √13

Length of  MN : 

M(0, -1) and N(-3, 1)

x₁ = 0, y₁ = -1, x₂ = -3 , y₂ = 1

MN = √[(-3 - 0)² + (1 + 1)²]

= √[(-3)² + (2)²]

 = √[9 + 4]

MN = √13

Length of  NK :

N(-3, 1) and K(-1, 4) 

x₁ = -3, y₁ = 1, x₂ = -1, y₂ = 4

NK = √[(-1 + 3)² + (4 - 1)²]

= √[(2)² + (3)²]

 = √[4 + 9]

NK = √13

KL = LM = MN = NK

c) Length of  KM :

K(-1, 4) and M(0, -1)

x₁ = -1, y₁ = 4, x₂ = 0, y₂ = -1

KM = √[(0 + 1)² + (-1 - 4)²]

= √[(1)² + (-5)²]

 = √[1 + 25]

KM = √26

Length of  NL :

N(-3, 1) and L(2, 2)

x₁ = -3, y₁ = 1, x₂ = 2, y₂ = 2

NL = √[(2 + 3)² + (2 - 1)²]

= √[(5)² + (1)²]

 = √[25 + 1]

NL = √26

KM = NL

So, diagonals are equal.