DETERMINE WHETHER THE TRIANGLES ARE SIMILAR

Write whether each pair of triangles are similar.

Problem 1 :

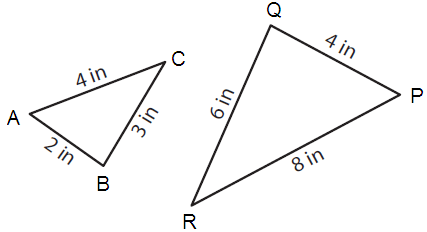
Solution :

(1) = (2) = (3)

AB/PQ = BC/QR = CA/RP = 1/2

By using Side – Side – Side theorem,

Since corresponding the sides are in the same ratio, triangles ABC and PQR similar.

Problem 2 :

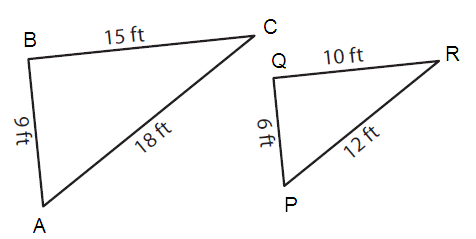
Solution :

AB/PQ = BC/QR = CA/RP = 3/2

Since, corresponding the sides are in the same ratio.

So, ∠ABC and ∠PQR similar.

Problem 3 :

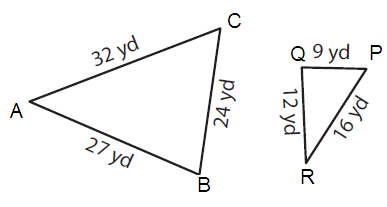
Solution :

Since the corresponding sides are not same, triangles ∠ABC and ∠PQR not similar.

Problem 4 :

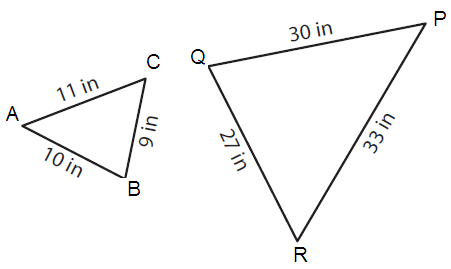
Solution :

AB/PQ = BC/QR = CA/RP = 1/3

Since the corresponding the sides are in the same ratio triangles ABC and PQR are similar.

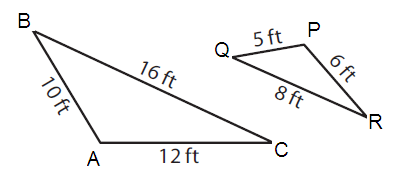
Problem 5 :

Solution :

AB/PQ = BC/QR = CA/RP = 2

Since, corresponding the sides are in the same ratio.

So, ∠ABC and ∠PQR similar.

Problem 6 :

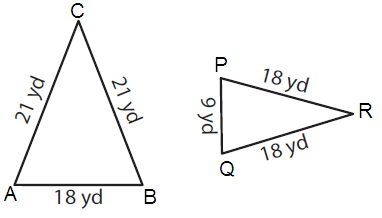
Solution :

Since corresponding the sides are not in the same ratio, triangles ABC and PQR not similar.

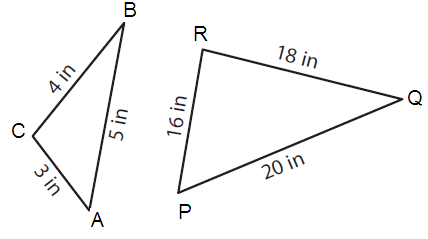
Problem 7 :

Solution :

Since corresponding the sides are not in the same ratio, triangles ABC and PQR not similar.

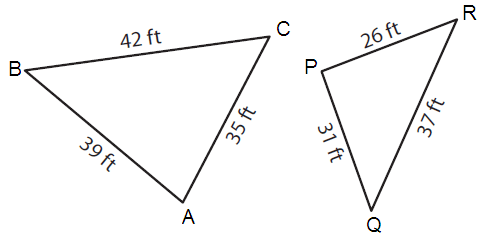
Problem 8 :

Solution :

Triangles ABC and PQR are not similar.

Problem 9 :

In the diagram, triangle DEF is similar to MNP. Find the value of x.

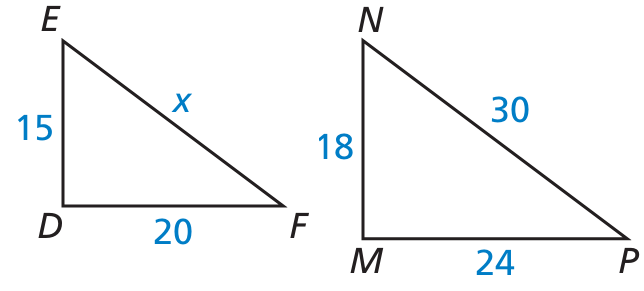
Solution :

DE/MN = DF/MP = EF/NP

15/18 = 20/24 = x/30

20/24 = x/30

20(30) = 24x

x = 20(30)/24

x = 25

So, the value of x is 25.

Problem 10 :

In the diagram, △TPR ∼ △XPZ. Find the length of the altitude PS.

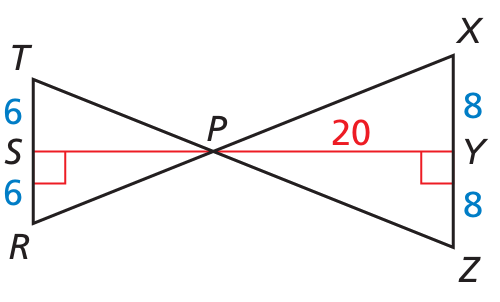
First, find the scale factor from △XPZ to △TPR.

TR/XZ = (6 + 6)/(8+8)

= 12/16

= 3/4

Because the ratio of the lengths of the altitudes in similar triangles is equal to the scale factor, you can write the following proportion.

PS/PY = 3/4

PS/20 = 3/4

PS = (3/4) (20)

PS = 3(5)

= 15

So, the length of PS is 15 cm.

Problem 11  :

A town plans to build a new swimming pool. An Olympic pool is rectangular with a length of 50 meters and a width of 25 meters. The new pool will be similar in shape to an Olympic pool but will have a length of 40 meters. Find the perimeters of an Olympic pool and the new pool.

Solution :

You are given the length and width of a rectangle and the length of a similar rectangle. You need to find the perimeters of both rectangles.

Find the scale factor of the similar rectangles and find the perimeter of an Olympic pool. Then use the Perimeters of Similar Polygons Theorem to write and solve a proportion to fi nd the perimeter of the new pool.

Solve the Problem Because the new pool will be similar to an Olympic pool, the scale factor is the ratio of the lengths, 40/50 = 4/5.

The perimeter of an Olympic pool is 2(50) + 2(25) = 150 meters.

Write and solve a proportion to fi nd the perimeter x of the new pool.

x/150 = 4/5

5x = 4(150)

x = 4(150) / 5

x = 4(30)

x = 120

So, the perimeter of an Olympic pool is 150 meters, and the perimeter of the new pool is 120 meters.

Problem 12  :

A school gymnasium is being remodeled. The basketball court will be similar to an NCAA basketball court, which has a length of 94 feet and a width of 50 feet. The school plans to make the width of the new court 45 feet. Find the perimeters of an NCAA court and of the new court in the school.

Solution :

Basketball court is similar to NCAA basketball court

Ratio between length and width of basket ball court = 94 : 50

Let x be the length of NCAA basket ball court.

Ratio between length and width of NCAA basket ball court = x : 45

94/50 = x/45

x = 94(45) / 50

x = 84.6

Perimeter of an NCAA court = 2(length + width)

= 2(84.6 + 45)

= 2(129.6)

= 259.2 square feet