DETERMINE THE EQUATION OF AXIS OF SYMMETRY

What is axis of symmetry ?

The axis of symmetry is the vertical line, which divides the parabola into two equal parts.

The axis of symmetry will always pass through the vertex of the parabola.

The quadratic function

y = ax² + bx + c

will have axis of symmetry at x = -b/2a

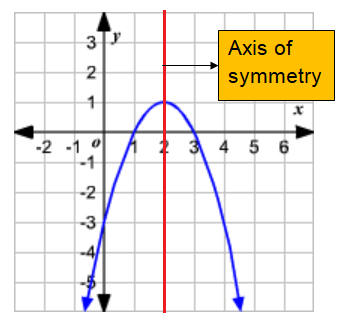
Determine the equation of the axis of symmetry of :

Problem 1 :

y = x² + 4x + 1

Solution :

Comparing the given equation with y = ax² + bx + c

a = 1, b = 4 and c = 1

Equation of axis of symmetry x = -b/2a

x = -4/2(1)

x = -4/2

x = -2

So, equation of axis of symmetry is at x = -2.

Problem 2 :

y = 2x² - 6x + 3

Solution :

Comparing the given equation with y = ax² + bx + c

a = 2, b = -6 and c = 3

Equation of axis of symmetry x = -b/2a

x = -6/2(2)

x = -6/4

x = -3/2

Problem 3 :

y = 3x² + 4x - 1

Solution :

Comparing the given equation with y = ax² + bx + c

a = 3, b = 4 and c = -1

Equation of axis of symmetry x = -b/2a

x = -4/2(3)

x = -4/6

x = -2/3

Problem 4 :

y = -x² - 4x + 5

Solution :

Comparing the given equation with y = ax² + bx + c

a = -1, b = -4 and c = 5

Equation of axis of symmetry x = -b/2a

x = -(-4)/2(-1)

x = -4/2

x = -2

Problem 5 :

y = -2x² + 5x + 1

Solution :

Comparing the given equation with y = ax² + bx + c

a = -2, b = 5 and c = 1

Equation of axis of symmetry x = -b/2a

x = 5/2(-2)

x = -5/4

x = -2

Problem 6 :

y = (1/2)x² - 10x + 2

Solution :

Comparing the given equation with y = ax² + bx + c

a = 1/2, b = -10 and c = 2

Equation of axis of symmetry x = -b/2a

x = -(-10)/2(1/2)

x = 10

Problem 7 :

y = (1/3)x² + 4x

Solution :

Comparing the given equation with y = ax² + bx + c

a = 1/3, b = 4 and c = 0

Equation of axis of symmetry x = -b/2a

x = -4/2(1/3)

x = -4(3/2)

x = -6

Problem 8 :

y = 100x - 4x²

Solution :

y = - 4x² + 100x 

Comparing the given equation with y = ax² + bx + c

a = -4, b = 100 and c = 0

Equation of axis of symmetry x = -b/2a

x = -100/2(-4)

x = 25/2

Problem 9 :

Tell whether the function f (x) = −4x² − 24x − 19 has a minimum value or a maximum value. Then find the value

Solution :

f(x) = −4x² − 24x − 19

By observing the given equation of parabola, it opens downward since the coefficient of x² is negative.

a = -4, b = -24 and c = -19

Equation of axis of symmetry x = -b/2a

x = -(-24)/2(-4)

x = 24/(-8)

x = -3

Maximum is at x = -3, to find the maximum value, we apply x = -3 in the function f(x).

f(-3) = −4(-3)² − 24(-3) − 19

= -4(9) + 72 - 19

= -36 - 19 + 72

= -55 + 72

f(-3) = 17

So, maximum value is 17.

Problem 10 :

The suspension cables between the two towers of the Mackinac Bridge in Michigan form a parabola that can be modeled by

y = 0.000098x² − 0.37x + 552

where x and y are measured in feet. What is the height of the cable above the water at its lowest point?

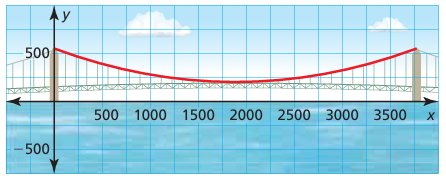
Solution :

y = 0.000098x² − 0.37x + 552

a = 0.000098, b = -0.37 and c = 552

x = -(-0.37) / 2(0.000098)

x = 0.37 / 0.000196

x = 1887.7

Approximately 1888.

Substitute 1888 for x in the equation to fi nd the y-coordinate of the vertex.

y = 0.000098(1888)² − 0.37(1888) + 552

≈ 203

The cable is about 203 feet above the water at its lowest point.

Problem 11 :

The function shown represents the height h (in feet) of a firework t seconds after it is launched. The firework explodes at its highest point.

a. When does the firework explode?

b. At what height does the firework explode?

Solution :

a)  By finding the maximum point of the curve, we will know that at which point the firework explode.

h = -16t² + 128t

a = -16, b = 128

x = -128/2(-16)

x = 128/32

x = 4

After 4 seconds the firework explode.

b) h = -16t² + 128t

when t = 4

h = -16(4)² + 128(4)

= -256 + 512

= 256 ft

Problem 12 :

The function h(t) = −16t² + 16t represents the height (in feet) of a horse t seconds after it jumps during a steeplechase.

a. When does the horse reach its maximum height?

b. Can the horse clear a fence that is 3.5 feet tall? If so, by how much?

c. How long is the horse in the air?

Solution :

h(t) = −16t² + 16t

a)  a = -16, b = 16 and c = 0

x = -16/2(-16)

= 16/32

x = 1/2

h(1/2) = -16(1/2)² + 16(1/2)

= -16/4 + 8

= -4 + 8

= 4

Maximum height is 4 feet.

b) By observing the maximum value, it is clear the horse can clear the fence that is 3.5 ft tall and by 0.5 feet.

c)  The horse is 0.5 seconds in the air.