DETERMINE IF THE FUNCTION IS EVEN OFF OR NEITHER WORKSHEET
Determine whether each function is even, odd, or neither.
Problem 1 :
g(x) = x³ - x
Problem 2 :
h(x) = x² + 1
Problem 3 :
f(x) = x³ - 1
Determine whether the function is even, odd, or neither. Then describe the symmetry.
Problem 4 :
f(x) = 5 - 3x
Problem 5 :
g(x) = x4 - x² - 1
Problem 6 :
h(x) = 2x³ + 3x
Problem 7 :
f(t) = t² + 2t - 3
Problem 8 :
g(x) = x³ - 5x
Problem 9 :
f(x) = x√1 - x²
Problem 10 :
f(x) = x√x + 5
Answer Key
1) The function g(x) is odd.
2) The function h(x) is even.
3) So, the function is neither even nor odd.
4) So, f(x) is neither even nor odd function.
5) So, g(x) is even function.
6) So, h(x) is odd function.
7) So, f(t) is neither even nor odd function.
8) So, g(x) is odd function.
9) So, f(x) is odd function.
10) f(x) is neither even nor odd function.
For each graph, determine whether the function is even, odd, or neither.
Problem 1 :
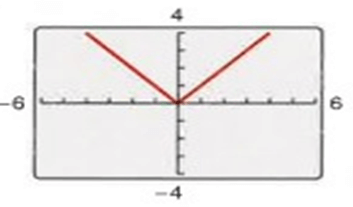
Problem 2 :
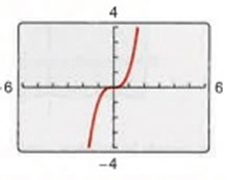
Problem 3 :
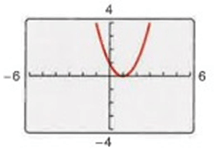
Problem 4 :
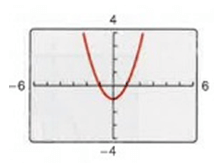
Answer Key
1) The graph is symmetric with respect to the y-axis. So, the function is even.
2) The graph is symmetric with respect to the origin. So, the function is odd.
3) So, the function is neither even nor odd.
4) The graph is symmetric with respect to the y-axis. So, the function is even.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling