DETERMINE IF THE FUNCTION IS DIFFERENTIABLE FROM THE GRAPH

Determine whether the following function is continuous, differentiable, neither or both at the point.

Problem 1 :

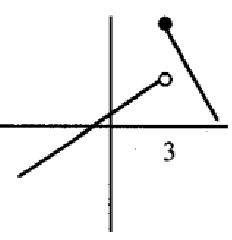
Solution :

The function is not continuous, it is not differentiable. It has jump discontinuity. So, it is neither.

Problem 2 :

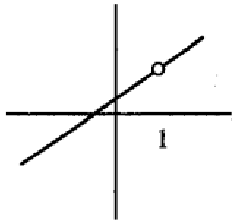
Solution :

The function has removable discontinuity. The function f(x) is discontinuous, then it is not differentiable.

So, it is neither.

Problem 3 :

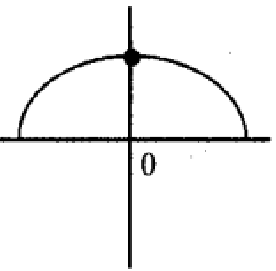
Solution :

The function is continuous, it is differentiable. So, it is both.

Problem 4 :

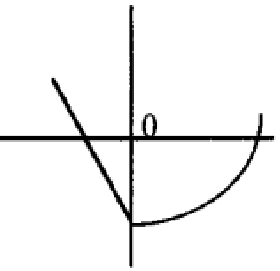
Solution :

The function is continuous, at x = 0, we see the vertical tangent. So, the function is continuous but not differentiable at the point x = 0.

Problem 5 :

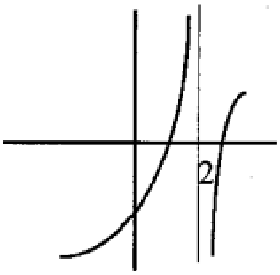
Solution :

The function is discontinuous at x = 2, it has infinite discontinuity. So, the function is discontinuous and it is not differentiable. Then it is both.

Problem 6 :

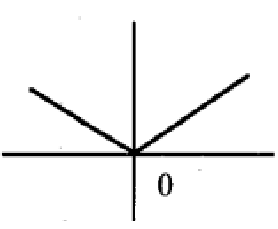
Solution :

The function is continuous. Since we have sharp point at x = 0. The function is not differentiable. So, the function is continuous but not differentiable.

Problem 7 :

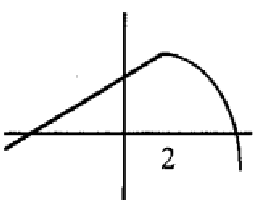
Solution :

The function is continuous. At x = 2, we can draw the vertical tangent line. Then the function is continuous but not differentiable at the point x = 2.

Problem 8 :

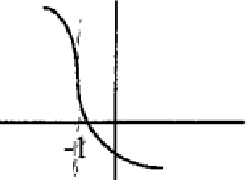
Solution :

The function is continuous. At x = -1, we can draw the vertical tangent line. Then the function is continuous but not differentiable at the point x = -1.