DESCRIBING TRANSFORMATIONS FROM THE GIVEN GIVEN GRAPH OF EXPONENTIAL FUNCTION

Transformations in Exponential Function

Compare each graph to f(x) = 2^x . Write a description of each transformation and graph each function.

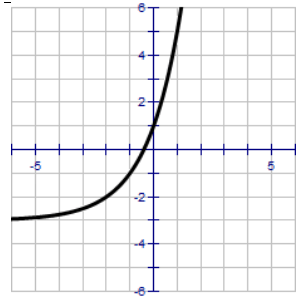
Problem 1 :

Solution :

Here the horizontal asymptote is y = -3

y = 2^{x - h} + (-3) ---(1)

The exponential curve is passing through the (1, 5).

5 = 2^{1 - h} + (-3)

8 = 2^{1 - h}

2³ = 2^{1 - h}

1 - h = 3

h = -2

By applying the value of h in (1), we get

y = 2^{x - (-2)} + (-3)

y = 2^{x + 2} - 3

Transformations done :

Moving the parent function y = 2^x,

2 units left and 3 units down

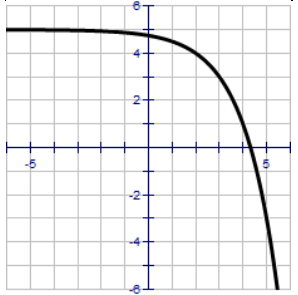
Problem 2 :

Solution :

Here the horizontal asymptote is y = 5. Observing the curve, it is reflected across x-axis.

y = -2^{x - h} + 5 ---(1)

The exponential curve is passing through the (2, 4).

4 = -2^{2 - h} + 5

-1 = -2^{2 - h}

-2⁰ = -2^{2 - h}

2 - h = 0

h = 2

By applying the value of h in (1), we get

y = -2^{x - 2} + 5

Transformations done :

Moving the parent function y = 2^x,

Reflection across x-axis, 2 units right and 5 units up.

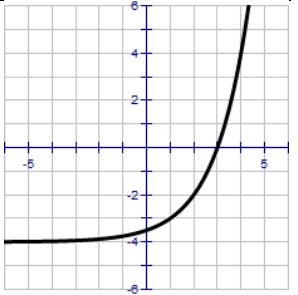
Problem 3 :

Solution :

Here the horizontal asymptote is y = -4.

y = 2^{x - h} + (-4) ---(1)

The exponential curve is passing through the (3, 0).

0 = 2^{3 - h} - 4

4 = 2^{3 - h}

2² = 2^{3 - h}

3 - h = 2

h = 3 - 2

h = 1

By applying the value of h in (1), we get

y = 2^{x - 1} - 4

Transformations done :

Moving the parent function y = 2^x,

1 unit right and 4 units down.

Problem 4 :

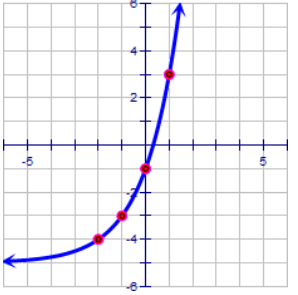
Solution :

Here the horizontal asymptote is y = -5.

y = 2^{x - h} + (-5) ---(1)

The exponential curve is passing through the (1, 3).

3 = 2^{1 - h} - 5

8 = 2^{1 - h}

2³ = 2^{1 - h}

1 - h = 3

h = 1 - 3

h = -2

By applying the value of h in (1), we get

y = 2^{x - (-2)} - 5

y = 2^{x + 2} - 5

Transformations done :

Moving the parent function y = 2^x,

2 unit left and 5 units down.

Problem 5 :

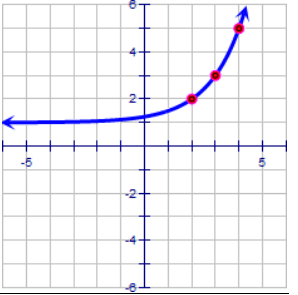
Solution :

Here the horizontal asymptote is y = 1.

y = 2^{x - h} + 1 ---(1)

The exponential curve is passing through the (1, 2).

2 = 2^{1 - h} + 1

1 = 2^{1 - h}

2⁰ = 2^{1 - h}

1 - h = 0

h = 1

By applying the value of h in (1), we get

y = 2^{x - 1} + 1

Transformations done :

Moving the parent function y = 2^x,

1 unit right and 1 unit up

Problem 6 :

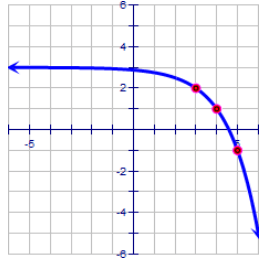
Solution :

Here the horizontal asymptote is y = 3. By observing the curve, it is reflected across x -axis

y = -2^{x - h} + 3 ---(1)

The exponential curve is passing through the (3, 2).

2 = -2^{3 - h} + 3

-1 = -2^{3 - h}

-2⁰ = -2^{3- h}

3 - h = 0

h = 3

By applying the value of h in (1), we get

y = -2^{x - 3} + 3

Transformations done :

Moving the parent function y = 2^x,

Reflected across x-axis, 3 units left and 3 unit up.

Problem 7 :

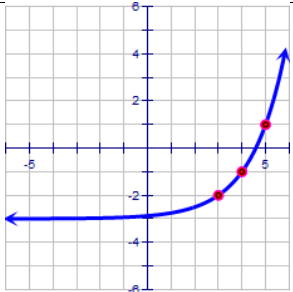
Solution :

Here the horizontal asymptote is y = -3. By observing the curve, it is reflected across x -axis

y = 2^{x - h} + (-3) ---(1)

The exponential curve is passing through the (3, -2).

-2 = 2^{3 - h} - 3

1 = 2^{3 - h}

2⁰ = 2^{3- h}

3 - h = 0

h = 3

By applying the value of h in (1), we get

y = 2^{x - 3} - 3

Transformations done :

Moving the parent function y = 2^x,

 3 units right and 3 unit down.

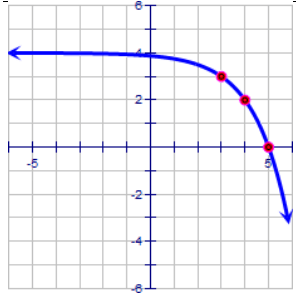
Problem 8 :

Solution :

Here the horizontal asymptote is y = 4. By observing the curve, it is reflected across x -axis

y = -2^{x - h} + 4 ---(1)

The exponential curve is passing through the (3, 3).

3 = -2^{3 - h} + 4

-1 = -2^{3 - h}

-2⁰ = -2^{3- h}

3 - h = 0

h = 3

By applying the value of h in (1), we get

y = -2^{x - 3} + 4

Transformations done :

Moving the parent function y = 2^x,

 3 units right and 4 units up.

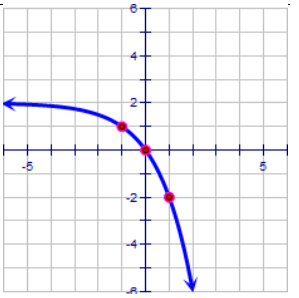
Problem 9 :

Solution :

Here the horizontal asymptote is y = 2. By observing the curve, it is reflected across x -axis

y = -2^{x - h} + 2 ---(1)

The exponential curve is passing through the (1, 1).

1 = -2^{1 - h} + 2

-1 = -2^{1 - h}

-2⁰ = -2^{1- h}

1 - h = 0

h = 1

By applying the value of h in (1), we get

y = -2^{x - 1} + 2

Transformations done :

Moving the parent function y = 2^x,

Reflected across x-axis,1 unit right and 2 units up.