DESCRIBING THE DOMAIN AND RANGE OF SQUARE ROOT FUNCTION

• The set of possible inputs for the function is known as domain.
• The set of possible outputs for the function is known as range. 

In general for the function y = √x

For the square root function, only positive values are possible values of x. For negative values, the function is undefined. So,

• Domain is [0, ∞)
• Range is [0, ∞).

From the function finding domain and range :

Fix the radicand ≥ 0 and solve for x.

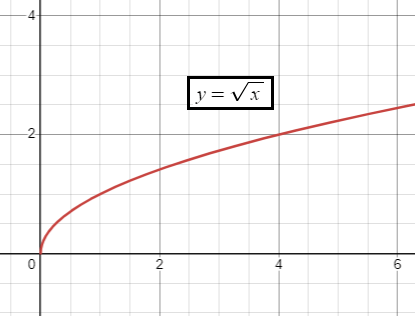	D is [0, ∞) R is [0, ∞)
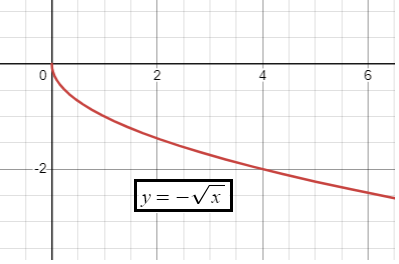	Reflection across x-axis, D is [0, ∞) R is (-∞, 0]
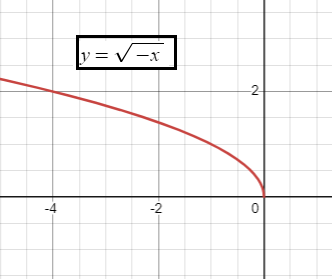	Reflection across y-axis, D is (-∞, 0] R is [0, ∞)

By finding horizontal asymptote, we can fix the starting point simply. From there we can fix the range.

For the function which is in the form 

y = a√b(x-h) + k

y = k is the horizontal asymptote.

Describe the domain of the function.

Problem 1 :

y = 8√x

Solution :

There is no reflection.

Domain :

√x ≥ 0

x ≥ 0

Domain is [0, ∞)

Range :

Horizontal asymptote is y = 0. The range is [0, ∞).

Problem 2 :

y = 4 + √-x

Solution :

There is reflection across y-axis.

Domain :

√-x ≥ 0

-x ≥ 0

x ≤ 0

Domain is (-∞, 0].

Range :

Horizontal asymptote is y = 4. The range is [4, ∞).

Problem 3 :

y = -√(x - 3)

Solution :

There is reflection across x-axis.

Domain :

√(x - 3) ≥ 0

x - 3 ≥ 0

x ≥ 3

Domain is [3, ∞).

Range :

Horizontal asymptote is y = 0. The range is (-∞, 0]

Problem 4 :

y = √(x + 2) - 2

Solution :

There is no reflection.

Domain :

√(x + 2) ≥ 0

x + 2 ≥ 0

x ≥ -2

Domain is [-2, ∞).

Range :

Horizontal asymptote is y = -2. The range is [-2, ∞).

Problem 5 :

y = √(-x - 1)

Solution :

y = √(-x - 1)

y = √-(x + 1)

There is reflection across y-axis.

Domain :

√-(x + 1) ≥ 0

-(x + 1) ≥ 0

(x + 1) ≤ 0

x ≤ -1

Domain is (-∞, -1].

Range :

Horizontal asymptote is y = 0. The range is [0, ∞).

Problem 6 :

y = √(2x) + 7

Solution :

There is no reflection

Domain :

√2x ≥ 0

2x ≥ 0

Dividing by 2 on both sides

x ≥ 0

Domain is [0, ∞).

Range :

Horizontal asymptote is y = 7. The range is [7, ∞).

Problem 7 :

y = (1/2)√(-x - 2)

Solution :

y = (1/2)√(-x - 2)

y = (1/2)√-(x + 2)

There is reflection across y-axis.

Domain :

√-(x + 2) ≥ 0

(x + 2) ≤ 0

x ≤ -2

Domain is (-∞, -2].

Range :

Horizontal asymptote is y = 0. The range is [0, ∞).