CROOK PROBLEMS

Problem 1 :

Find x in the following.

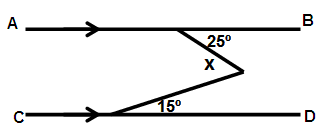
Solution:

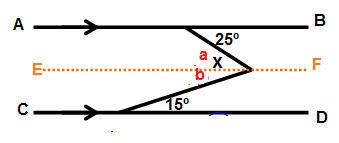
Drawing a line EF which is parallel to AB and CD.

Alternate interior angle will be equal to a and b.

a = 25˚ and b = 15˚

x = a + b 

x = 25˚ + 15˚

x = 40˚

Problem 2 :

Find x in the following.

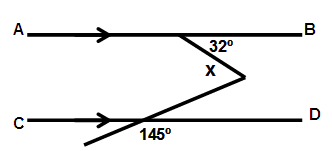
Solution:

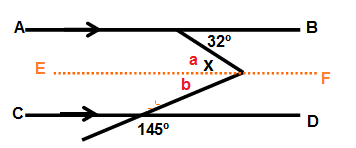
Drawing a line E and F which is parallel to AB and CD.

 a = 32˚ (Alternate interior angle)

145˚ = 180˚ - b

b = 180˚ - 145˚

b = 35˚

x = a + b

x = 32˚ + 35˚

x = 67˚

Problem 3 :

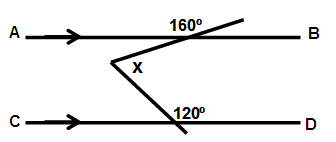
Solution:

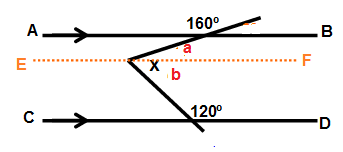
Drawing a line EF which is parallel to AB and CD.

a = 180 - 160

a = 20˚

b = 180 - 120

b = 60˚

x = a + b

x = 20˚ + 60˚

x = 80˚

Problem 4 :

Find the value of x.

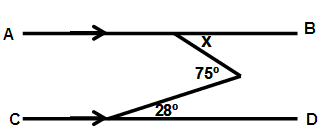
Solution:

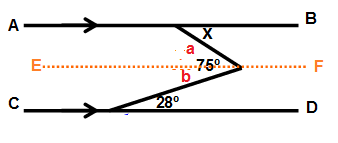
Drawing a line E and F which is parallel to AB and CD.

b = 28˚ (Alternate interior angle)

75˚ = a + b

75˚ = x + 28˚

x = 75 - 28

x = 47˚ 

Problem 5 :

Find x in the following.

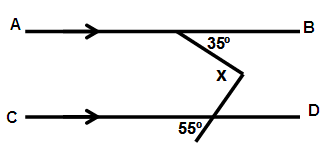
Solution:

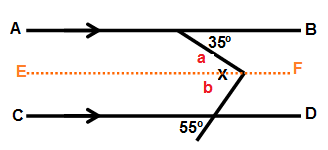
Drawing a line EF which is parallel to AB and CD.

Alternate interior angle will be equal to a and b.

a = 35˚ and b = 55˚

x = a + b 

x = 35˚ + 55˚

x = 90˚

Problem 6 :

Find x in the following.

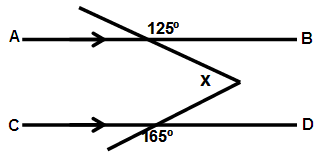
Solution :

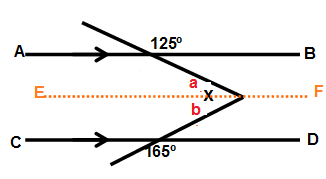
Drawing a line E and F which is parallel to AB and CD.

125 + a = 180

a = 180 - 125

a = 55

165 + b = 180

b = 180 - 165

b = 15

x = a + b

x = 55˚ + 15˚

x = 70˚

Problem 7 :

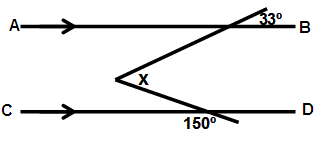
Solution:

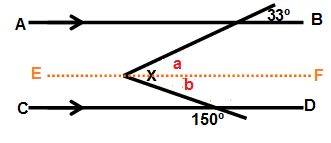
Drawing a line E and F which is parallel to AB and CD.

a = 33˚ (Alternate interior angle)

150 + b = 180

b = 180 - 150

b = 30

x = a + b

x = 33 + 30

x = 63

Problem 8 :

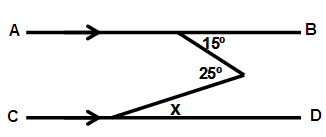
Solution:

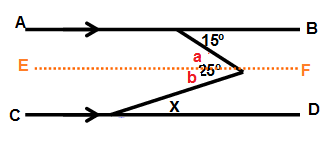
Drawing a line E and F which is parallel to AB and CD.

a = 15˚ (Alternate interior angle)

a + 25 = b

15 + 25 = b

b = 40

x = a + b

x = 15 + 40

z = 55

Problem 9 :

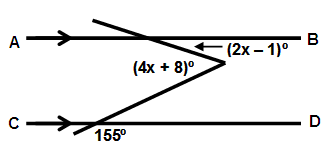
Solution:

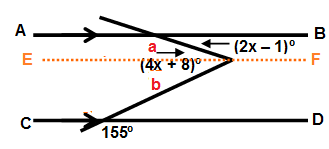
Drawing a line EF which is parallel to AB and CD.

155 + b = 180

b = 180 - 155

b = 25

a + b = 4x + 8

2x - 1 + 25 = 4x + 8

2x - 4x = 8 - 24

-2x = -16

x = 8

Problem 10 :

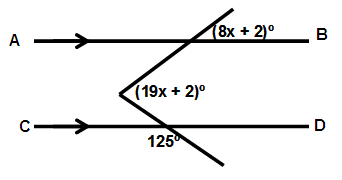
Solution:

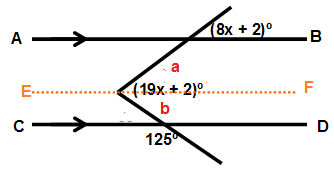
Drawing a line E and F which is parallel to AB and CD.

125 + b = 180

b = 180 - 125

b = 55

a = 8x + 2

a + b = 19x + 2

8x + 2 + 55 = 19x + 2

8x - 19x = 2 - 2 - 55

-11x = -55

x = 5