CREATE A QUADRATIC FUNCTION FROM THE GIVEN ZEROS

Problem 1 :

Write a quadratic equation in standard form with solutions, x = -3 and x = 4. Use integers for a, b and c.

Solution:

Sum of the roots :

= -3 + 4

= 1

Product of the roots :

= -3 × 4

= -12

Formation of quadratic equation:

x² - (sum of the roots)x + product of the roots = 0

x² - x - 12 = 0

Problem 2 :

Write a quadratic equation in standard form with solutions, x = 2/3 and x = -5. Use integers for a, b and c.

Solution:

Sum of the roots :

= (2/3) + (-5)

= (2/3) - 5

= (2 - 15)/3

= -13/3

Product of the roots :

= (2/3) × (-5)

= -10/3

Formation of quadratic equation:

x² - (sum of the roots)x + product of the roots = 0

x² - (-13/3)x + (-10/3) = 0

x² + (13/3)x - (10/3) = 0

Multiply each side by 3.

3x² + 13x - 10 = 0

Problem 3 :

Write an equation of the parabola in intercept form y = a(x - p)(x - q) that has x- intercepts of 9 and 1 and passes through (0, -18).

A) y = -1/2(x - 9)(x - 1)              B) y = -1/2(x + 9)(x + 1)

C) y = -2(x - 9)(x - 1)                 D) y = -2(x + 9)(x + 1)

Solution:

y = a(x - p)(x - q)

Using the given x-intercepts, we can write

y = a(x - 9)(x - 1)

It is passes through the point (x, y) = (0, -18).

-18 = a(0 - 9)(0 - 1)

-18 = a(-9)(-1)

-18 = 9a

a = -2

So, the equation of the parabola in intercept form is

y = -2(x - 9)(x - 1)

So, option (C) is correct.

Problem 4 :

Write an equation of the parabola in intercept form y = a(x - p)(x - q) that has x- intercepts of 12 and -6 and passes through (14, 4).

A) y = 1/10(x - 12)(x + 6)      B) y = 1/10(x + 12)(x - 6)

C) y = 10(x - 12)(x + 6)         D) y = 10(x + 12)(x - 6)

Solution:

y = a(x - p)(x - q)

Using the given x-intercepts, we can write

y = a(x - 12)(x + 6)

It is passes through the point (x, y) = (14, 4).

4 = a(14 - 12)(14 + 6)

4 = a(2)(20)

4 = 40a

a = 1/10

So, the equation of the parabola in intercept form is

y = 1/10(x - 12)(x + 6)

So, option (A) is correct.

Problem 5 :

Determine the equation of a quadratic function given zeros x = 4 and point (3, 2).

Solution:

y = a(x - p)(x - q)

Given x- intercept = 4

y = a(x - 4)(x - 4)

To find a, substitute the point (x, y) = (3, 2).

2 = a(3 - 4)(3 - 4)

2 = a(-1)(-1)

 a = 2

y = 2(x - 4)(x - 4)

Problem 6 :

Use the intercepts and a point on the graph below to write the equation of the function.

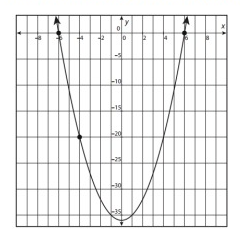
Solution:

y = a(x - p)(x - q)

x- intercept = (-6, 0) and (6, 0)

y = a(x + 6)(x - 6)

To find a, substitute the point (x, y) = (-4, -20).

-20 = a(-4 + 6)(-4 - 6)

-20 = a(2)(-10)

-20= -20a

 a = 1

y = (x + 6)(x - 6)

Problem 7 :

Use the intercepts and a point on the graph below to write the equation of the function.

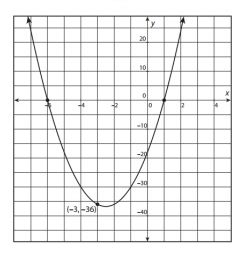
Solution:

y = a(x - p)(x - q)

x- intercept = (-6, 0) and (1, 0)

y = a(x + 6)(x - 1)

To find a, substitute the point (x, y) = (-3, -36).

-36 = a(-3 + 6)(-3 - 1)

-36 = a(3)(-4)

-36= -12a

 a = 3

y = 3(x + 6)(x - 1)