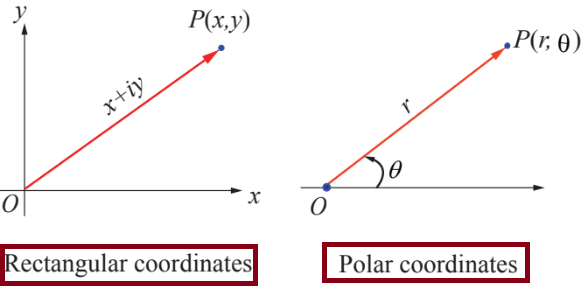
CONVERTING RECTANGULAR FORM TO POLAR FORM

Let r and θ be polar coordinates of the point P(x, y) that corresponds to a non zero complex number z = x + iy.

The real number θ represents the angle, measured in radians, that z makes with the positive real axis when z is interpreted as a radius vector.

The angle θ has an infinitely many possible values, including negative ones that differ by integral multiples of 2π.

Those values can be determined from the equation

tan θ = y/x.

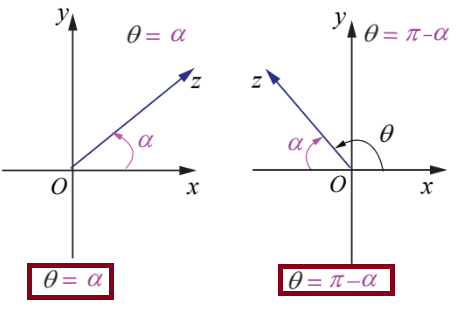
• The required angle lies in the 1^st quadrant, then θ = α
• The required angle lies in the 2^nd quadrant, then 

θ = π-α

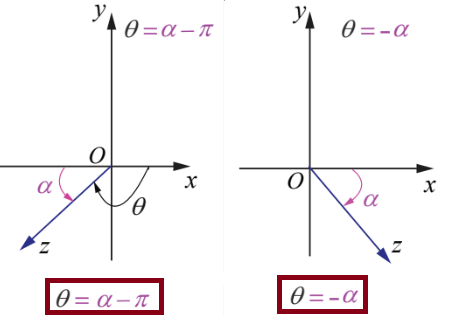
• The required angle lies in the 3^rd quadrant, then

 θ = -π+α

• The required angle lies in the 4^th quadrant, then

 θ = -α

Find the polar coordinates of the point with the given rectangular coordinates

Problem 1 :

(-5, 12)

Solution :

Rectangular form (x, y) ==> (-5, 12)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √(-5)² + 12²

r = √(25 + 144)

r = √169

r = 13

Finding θ :

θ = tan^-1(y/x)

x = -5 and y = 12

θ lies in the 2^nd quadrant

θ = π - α

α = tan^-1(12/5)

θ = π - tan^-1(12/5)

θ = 180 - 67.38

θ = 112.62

So, the required polar coordinate is ( 13, 112.62 ).

Problem 2 :

(3, -3)

Solution :

Rectangular form (x, y) ==> (-3, 3)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √3² + (-3)²

r = √(9+9)

r = √18

r = 3√2

Finding θ :

α = tan^-1(y/x)

x = 3 and y = -3

θ lies in the 4th quadrant.

θ = -α

θ = -tan^-1(3/3)

θ = -tan^-1(1)

θ = -π/4

So, the required polar coordinate is (3√2, -π/4).

Problem 3 :

(-2, -2√3)

Solution :

Rectangular form (x, y) ==> (-2, -2√3)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √(-2)² + (-2√3)²

r = √(4+12)

r = √16

r = 4

Finding θ :

θ = tan^-1(y/x)

x = -2 and y = -2√3

θ lies in 3rd quadrant.

α = tan^-1(2√3/2)

α = tan^-1(√3)

α = π/3

θ = (π/3) - π

θ = (-2π/3)

So, the required polar coordinate is (4, (-2π/3)).

Problem 4 :

(0, -3)

Solution :

Rectangular form (x, y) ==> (0, -3)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √0² + (-3)²

r = √9

r = 3

Finding θ :

θ = tan^-1(y/x)

x = 0 and y = -3

α = tan^-1(0/3

α = tan^-1(0)

α = 0

θ = 0 - π

θ = -π

So, the required polar coordinate is (3, -π).

Problem 5 :

(5, 5)

Solution :

Rectangular form (x, y) ==> (5, 5)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √5² + 5²

r = 5√2

Finding θ :

θ = tan^-1(y/x)

x = 5 and y = 5

θ lies in the first quadrant.

α = tan^-1(5/5)

α = tan^-1(1)

α = π/4

θ = π/4

So, the required polar coordinate is (5√2, π/4).

Problem 6 :

(-1, √3)

Solution :

Rectangular form (x, y) ==> (-1, √3)

Polar form (r, θ) ==> ?

Finding r :

r = √(x² + y²)

r = √(-1)² + (√3)²

r = √(1 + 3)

r = 2

Finding θ :

θ = tan^-1(y/x)

x = -1 and y = √3

θ lies in the second quadrant.

α = tan^-1(√3/1)

α = tan^-1(√3)

α = π/3

θ = π - (π/3)

θ = 2π/3

So, the required polar coordinate is (2, 2π/3).