CONVERTING QUADRATIC TO VERTEX FORM AND GRAPH

Solve the equation by rewriting in vertex (h, k) form. Sketch a graph and label the vertex and x - intercepts.

Problem 1 :

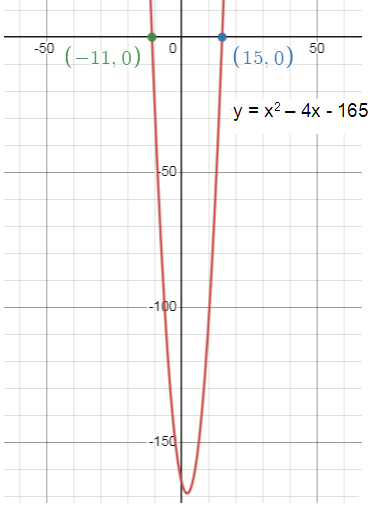
y = x² - 4x - 165

1. find vertex form  2. find x - intercepts  3. graph completely

Solution :

1. Vertex form

y = x² - 4x - 165

Using completing the square method,

y = x² - 2·x·2 + 2² - 2² - 165

y = (x - 2)² - 2² - 165

y = (x - 2)² - 4 - 165

y = (x - 2)² - 169

The vertex form of y = (x - 2)² - 169

Vertex is at (2, -169)

2. To find x - intercepts

y = x² - 4x - 165

Put y = 0

x² - 4x - 165 = 0

x² + 11x - 15x - 165 = 0

x(x + 11) - 15(x + 11) = 0

(x - 15) and (x + 11) = 0

x - intercept are (15, 0) and (-11, 0).

3. Graph

Problem 2 :

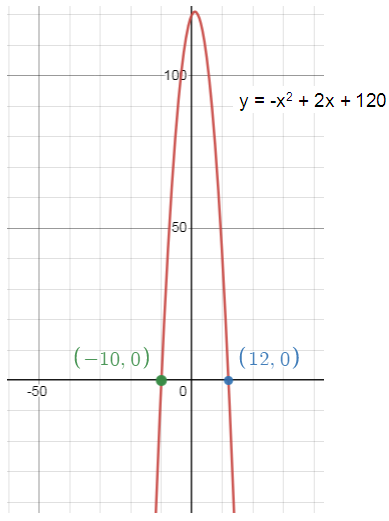
f(x) = -x² + 2x + 120

1. find vertex form  2. find x - intercepts  3. graph completely

Solution :

1. Vertex form

f(x) = -x² + 2x + 120

f(x) = -(x² - 2x) + 120

f(x) = -(x² - 2·x·1 + 1² - 1²) + 120

f(x) = -[(x - 1)² - 1²] + 120

f(x) = -(x - 1)² + 1 + 120

f(x) = -(x - 1)² + 121

The vertex form of f(x) = -(x - 1)² + 121.

2. To find x - intercepts

f(x) = -x² + 2x + 120

f(x) = -(x² - 2x - 120)

-f(x) =  x² - 2x - 120 

Put f(x) = 0

x² - 2x - 120 = 0

x² + 10x - 12x - 120 = 0

x(x + 10) - 12(x + 10) = 0

(x - 12) and (x + 10) = 0

x - intercepts are (12, 0) and (-10, 0).

3. Graph

Problem 3 :

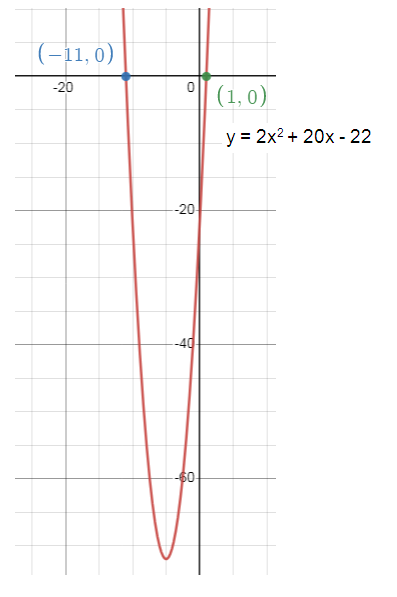
y = 2x² + 20x - 22

1. find vertex form  2. find x - intercepts  3. graph completely

Solution :

1. Vertex form

y = 2x² + 20x - 22

y = 2(x² + 10x) - 22

y = 2(x² + 2·x·5 + 5² - 5²) - 22

y = 2[(x + 5)² - 25] - 22

y = 2(x + 5)² - 50 - 22

y = 2(x + 5)² - 72

The coordinates of the vertex is (-5, -72) = (h, k)

2. To find x - intercepts

y = 2x² + 20x - 22

Put y = 0

2x² + 20x - 22 = 0

2(x² + 10x - 11) = 0

x² + 10x - 11 = 0

x² - x + 11x - 11 = 0

x(x - 1) + 11(x - 1) = 0

(x + 11) and (x - 1) = 0

x - intercepts are (-11, 0) and (1, 0).

3. Graph

Problem 4 :

Which correctly identifies the values of the parameters a, h, and k for the function f(x) = -2(x + 3)² + 1

Solution :

Given, function f(x) = -2(x + 3)² + 1

The vertex form is y = a(x - h)² + k, where (h, k) are the coordinates of the vertex.

For the given function a = -2, h = -3 and k = 1

So, option c) is correct.

Problem 5 :

Kevin threw a ball straight up with an initial speed of 20 meters per second. The function

y = -5(x - 2)² + 20

describe the ball’s height, in meters, t seconds after Kevin threw it. What are the coordinates of the vertex ?

Solution :

Given function is  y = -5(x - 2)² + 20

The vertex form is y = (x - h)² + k, where (h, k) are the coordinates of the vertex.

The coordinates of the vertex are (2, 20).

So, option b) is correct.

Problem 6 :

Which equation describes a parabola that opens downward, is congruent to y = x², and has its vertex at (0, 3) ?

Solution :

The vertex of the parabola is at (0, 3).

Because the constant term in the equation represents the y-coordinate of the vertex.

Given, y = x²

y - 3 = -(x - 0)²

y - 3 = -x²

y = -x² + 3

Problem 7 :

Which of following functions does NOT represent the parabola with a vertex at (1, 4) and x – intercepts (-1, 0) and (3, 0).

Solution :

Let us consider the quadratic function as

y = a(x - h)² + k

y = a(x - 1)² + 4

Applying x-intercepts, (1, 0) and (3, 0)

0 = a(3 - 1)² + 4

0 = a(4) + 4

-4 = 4a

a = -1

y = -1(x - 1)² + 4

Problem 8 :

Given the function,

f(x) = x² + 10x + 23

state whether the parabola opens up or down and the maximum or minimum value.

Solution :

Given the function, f(x) = x² + 10x + 23 

The equation of a parabola which will open upward (because of the positive coefficient of x²)

So, it will have a minimum value.

Problem 9 :

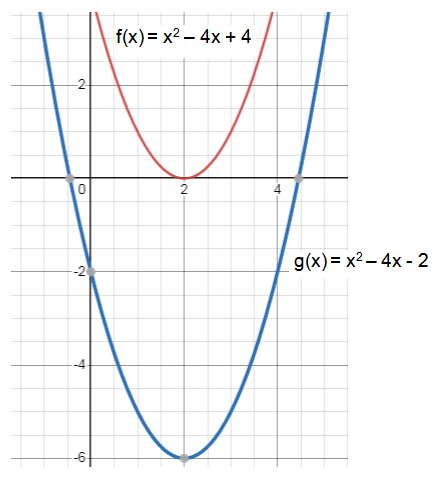
Compare the functions, f(x) and g(x), and explain how the graph of f(x) = x² – 4x + 4 is related to the graph of g(x) = x² – 4x - 2.

A. f(x) is vertically stretched to make g(x)

B. f(x) is translated 6 units left to make g(x)

C. f(x) is translated down 6 units to make g(x)

D. f(x) is compressed vertically to make g(x)

Solution :

Translating down 6 units.