CONVERTING FROM STANDARD FORM TO VERTEX FORM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Use the information provided to write the vertex form equation of each parabola.
Problem 1 :
y = x2 - 4x + 5
Solution :
Step 1 :
The coefficient of x2 is 1.
Step 2 :
Subtract 5 on both sides.
y - 5 = x2 - 4x + 5 - 5
y - 5 = x2 - 4x
Step 3 :
Half of the coefficient of x is 2
Square of half of the coefficient of x is 22 = 4
y - 5 + 4 = x2 - 4x + 4
y - 5 + 4 = x2 - 2 ⋅ x ⋅ 2 + 22
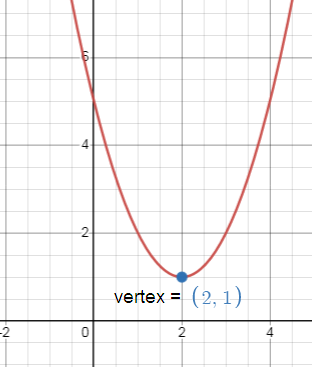
y - 1 = (x - 2)2
Step 4 :
By comparing the above equation with vertex form
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (2, 1)
Since the coefficient of x2 is positive the parabola opens upward.
Use the information provided to write the vertex form equation of each parabola.
Problem 2 :
y = x2 - 16x + 70
Solution :
Step 1 :
The coefficient of x2 is 1.
Step 2 :
Subtract 70 on both sides.
y - 70 = x2 - 16x + 70 - 70
y - 70 = x2 - 16x
Step 3 :
Half of the coefficient of x is 8
Square of half of the coefficient of x is 82 = 64
y - 70 + 64 = x2 - 16x + 64
y - 6 = x2 - 2 ⋅ x ⋅ 8 + 64
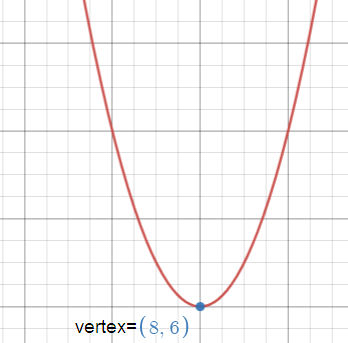
y - 6 = (x - 8)2
Step 4 :
By comparing the above equation with vertex form
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (8, 6)
Since the coefficient of x2 is positive the parabola opens upward.
Problem 3 :
y = x2 - 4x + 2
Solution :
Step 1 :
The coefficient of x2 is 1.
Step 2 :
Subtract 2 on both sides.
y - 2 = x2 - 4x + 2 - 2
y - 2 = x2 - 4x
Step 3 :
Half of the coefficient of x is 2
Square of half of the coefficient of x is 22 = 4
y - 2 + 4 = x2 - 4x + 4
y - 2 + 4 = x2 - 2 ⋅ x ⋅ 2 + 22
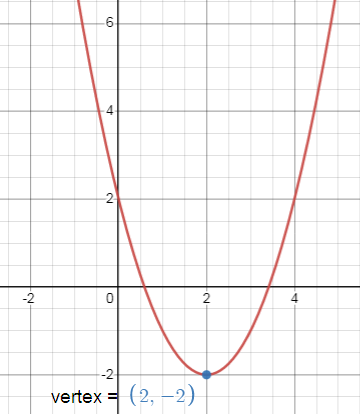
y + 2 = (x - 2)2
Step 4 :
By comparing the above equation with vertex form
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (2, -2)
Since the coefficient of x2 is positive the parabola opens upward.
Problem 4 :
y = -3x2 + 48x - 187
Solution :
y = -3x2 + 48x - 187
y = -3[x2 - 16x] - 187
Step 1 :
The coefficient of x2 is not 1.
Step 2 :
Adding 187 on both sides.
y + 187 = -3[x2 - 16x] - 187 + 187
y + 187 = -3[x2 - 16x]
y + 187 = -3(x2 - 2 ⋅ x ⋅ 8 + 82 - 82)
y + 187 = -3[(x - 8)2 - 64]
y + 187 = -3(x - 8)2 + 192
y + 187 - 192 = -3(x - 8)2
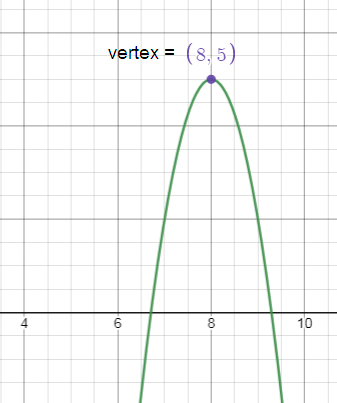
y - 5 = -3(x - 8)2
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (8, 5)
Since the coefficient of x2 is negative the parabola opens downward.
Problem 5 :
y = -2x2 - 12x - 12
Solution :
y = -2x2 - 12x - 12
Step 1 :
The coefficient of x2 is not 1.
Step 2 :
Adding 12 on each sides.
y + 12 = -2x2 - 12x
y + 12= -2[x2 + 6x]
y + 12 = -2(x2 + 2 ⋅ x ⋅ 3 + 32 - 32)
y + 12 = -2[(x + 3)2 - 9]
y + 12 = -2(x + 3)2 + 18
y + 12 - 18 = -2(x + 3)2
y - 6 = -2(x + 3)2
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (-3, 6)
Since the coefficient of x2 is negative the parabola opens downward.
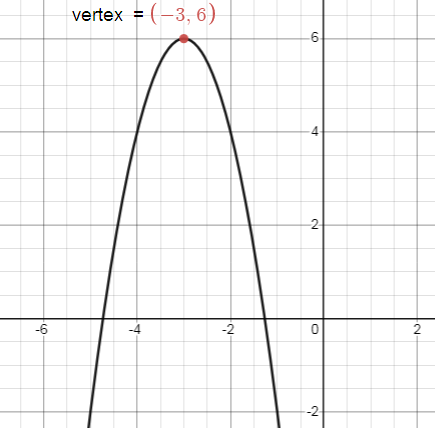
Problem 6 :
y = 3x2 + 18x + 18
Solution :
y = 3x2 + 18x + 18
Step 1 :
The coefficient of x2 is not 1.
Step 2 :
Subtracting 18 on each sides.
y - 18 = 3x2 + 18x
y - 18= 3[x2 + 6x]
y - 18 = 3(x2 + 2 ⋅ x ⋅ 3 + 32 - 32)
y - 18 = 3[(x + 3)2 - 9]
y - 18 = 3(x + 3)2 - 27
y - 18 + 27 = 3(x + 3)2
y + 9 = 3(x + 3)2
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (-3, -9)
Since the coefficient of x2 is positive the parabola opens upward.
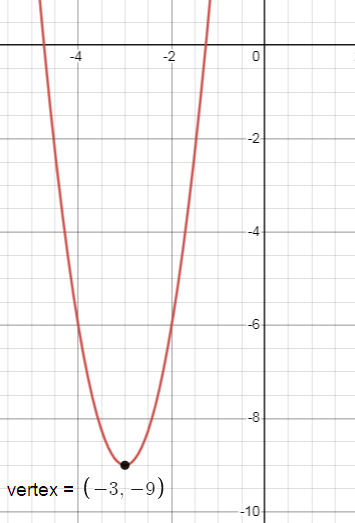
Problem 7 :
y = 2x2 + 3
Solution :
y = 2x2 + 0x + 3
Step 1 :
The coefficient of x2 is not 1.
Step 2 :
Subtracting 3 on each sides.
y - 3 = 2x2 + 0x
y - 3= x[2x + 0]
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (0, 3)
Since the coefficient of x2 is positive the parabola opens upward.
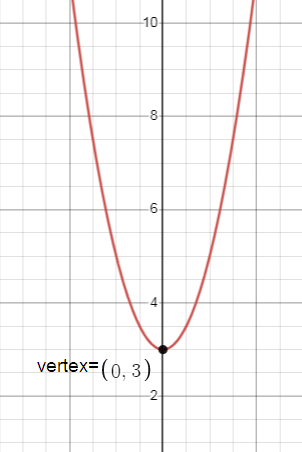
Problem 8 :
y = 4x2 - 56x + 200
Solution :
y = 4x2 - 56x + 200
Step 1 :
The coefficient of x2 is not 1.
Step 2 :
Subtracting 200 on each sides.
y - 200 = 4x2 - 56x
y - 200= 4[x2 - 14x]
y - 200 = 4(x2 - 2 ⋅ x ⋅ 7 + 72 - 72)
y - 200= 4[(x - 7)2 - 49]
y - 200 = 4(x - 7)2 - 196
y - 200 + 196 = 4(x - 7)2
y - 4 = 4(x - 7)2
(y - k) = a(x - h)2
We can get the vertex.
(h, k) = (7, 4)
Since the coefficient of x2 is positive the parabola opens upward.
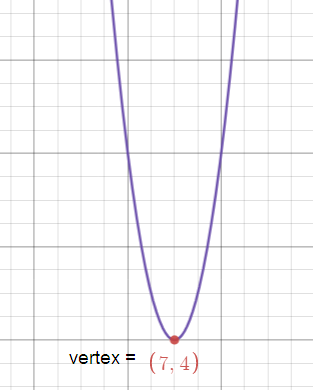
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling