Converting Between Standard Vertex and Factored Form

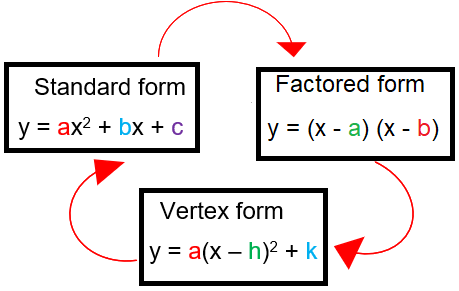
Given one of the forms of a quadratic function, convert to the other two forms.

Problem 1 :

y = x² − 6x − 7

(i) Vertex form

(ii)  Factored form

Solution :

(i) Converting into vertex form :

y = x² − 6x − 7

Coefficient of x² is 1. So, don't have to factories anything.

Write the coefficient of x as multiple of 2. 

y = x² − 2⋅x⋅3 + 3² - 3² - 7

y = (x - 3)² - 3² - 7

y = (x - 3)² - 9 - 7

y = (x - 3)² - 16

y = (x - h)² + k

Vertex (h, k) is (3, -16).

(i) Converting into factored form :

y = x² − 6x − 7

Decomposing -7, we get 1 (-7).

1(-7) = -7, 1 + (-7) = -6

y = x² + 1x - 7x − 7

y = x(x + 1) - 7(x + 1)

y = (x + 1) (x - 7)

So, -1 and 7 are x-intercepts.

Problem 2 :

y = 3(x − 1)² − 3

(i) Standard form 

(ii) Factored form

Solution :

(i) Converting into standard form :

y = 3(x − 1)² − 3

Here (x-1)² looks like (a - b)².

(a - b)² = a² - 2ab + b²

(x − 1)² = x² - 2x(1) + 1²

(x − 1)² = x² - 2x - 3

y = 3(x² - 2x + 1) - 3

y = 3x² - 6x + 3 - 3

y = 3x² - 6x

(ii) Converting into factored form :

y = 3x² - 6x

Factor 3x, we get

= 3x (x - 2)

So, 0 and 2 are x-intercepts.

Problem 3 :

y = 2(x − 3)(x + 5)

(i) Vertex form:

(ii) Standard form:

Solution :

(i) Converting into vertex form :

y = 2(x − 3)(x + 5)

y = 2(x² + 5x - 3x - 15)

y = 2(x² + 2x - 15)

y = 2(x² + 2⋅x⋅1 + 1² - 1² - 15)

y = 2[(x + 1)² - 1² - 15]

y = 2[(x + 1)² - 16]

y = 2(x + 1)² - 32

So, vertex is (-1, -32).

(ii) Converting into standard form :

y = 2(x − 3)(x + 5)

y = 2(x − 3)(x + 5)

y = 2(x² + 5x - 3x - 15)

y = 2(x² + 2x - 15)

Distributing 2, we get

y = 2x² + 4x - 30

Problem 4 :

y = 2x² + 8x + 10

(i) Vertex form:

(ii) Factored form

Solution :

(i) Converting into vertex form :

y = 2x² + 8x - 10

y = 2(x² + 4x - 5)

y = 2(x² + 2⋅x⋅2 + 2² - 2² - 5)

y = 2[(x+2)² - 4 - 5)]

y = 2[(x+2)² - 9]

y = 2(x+2)² - 18

So, the vertex is (-2, -18).

(ii) Converting into factored form :

y = 2x² + 8x - 10

y = 2(x² + 4x - 5)

y = 2(x - 5² + 4x - 5)

Problem 5 :

𝑦 = 2(𝑥 + 1)² − 8

(i)  Standard form

(ii)  Factored form

Solution :

(i) Converting into standard form :

𝑦 = 2(𝑥 + 1)² − 8

Using the algebraic identity (a + b)², we can find the expansion of (x + 1)²

(x + 1)² = x² + 2⋅x⋅1 + 1²

(x + 1)² = x² + 2x + 1

y = 2(x² + 2x + 1) − 8

y = 2x² + 4x + 2 − 8

y = 2x² + 4x − 6

(ii) Converting into factored form :

y = 2x² + 4x − 6

Factoring 2, we get

y = 2(x² + 2x − 3)

y = 2(x - 1) (x + 3)

Problem 6 :

y = −4(x + 1)(2x − 5)

(i) Vertex form:

(ii)  Standard form:

Solution :

(i) Converting into vertex form :

y = −4(x + 1)(2x − 5)

y = −4(2x² - 5x + 2x - 5)

y = −4(2x² - 3x - 5)

y = −4(2x² - 3x - 5)

So, the vertex is (3/4, 49/2).

(ii) Converting into standard form :

y = −4(x + 1)(2x − 5)

y = −4(2x² - 5x + 2x - 5)

y = −4(2x² - 3x - 5)

y = −4(2x² - 3x - 5)

y = −8x² + 12x + 20