CONVERTING ABSOLUTE VALUE FUNCTIONS TO PIECEWISE DEFINED FUNCTION
For each of the functions, create a piecewise definition.
Problem 1 :
f(x) = |x - 1|
Solution :
f(x) = |x - 1|
f(x) = x - 1 and f(x) = -(x - 1)
Case 1 :
f(x) = x - 1
when x ≥ 1, f(x) is positive
Case 2 :
f(x) = -(x - 1)
when x < 1, f(x) is negative
Distributing negative, we get
f(x) = - x + 1
So, the required definition is
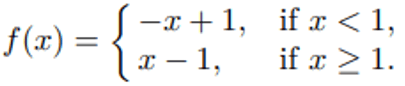
Problem 2 :
f(x) = |x + 2|
Solution :
f(x) = |x + 2|
f(x) = x + 2 and f(x) = -(x + 2)
Let f(x) = 0
x + 2 = 0
x = -2
Case 1 :
f(x) = x + 2
when x ≥ -2, f(x) is positive
Case 2 :
f(x) = -(x + 2)
when x < -2, f(x) is negative
Distributing negative, we get
f(x) = - x - 2
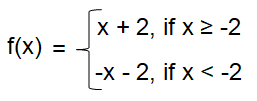
Problem 3 :
f(x) = |2x - 1|
Solution :
f(x) = |2x - 1|
f(x) = 2x - 1 and f(x) = -(2x - 1)
Let f(x) = 0
2x - 1 = 0
x = 1/2
Case 1 :
f(x) = 2x - 1
when x ≥ 1/2, f(x) is positive
Case 2 :
f(x) = -(2x - 1)
when x < 1/2, f(x) is negative
Distributing negative, we get
f(x) = - 2x + 1
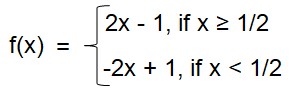
Problem 4 :
f(x) = |5 - 2x|
Solution :
f(x) = |5 - 2x|
f(x) = 5 - 2x and f(x) = -(5 - 2x)
Let f(x) = 0
5 - 2x = 0
2x = 5
x = 5/2
Case 1 :
f(x) = 5 - 2x
when x ≤ 5/2, f(x) is positive
Case 2 :
f(x) = -(5 - 2x)
when x > 5/2, f(x) is negative
Distributing negative, we get
f(x) = -5 + 2x or 2x - 5
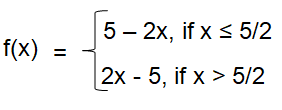
Problem 5 :
f(x) = |1 - 3x|
Solution :
f(x) = |1 - 3x|
f(x) = 1 - 3x and f(x) = -(1 - 3x)
Let f(x) = 0
1 - 3x = 0
3x = 1
x = 1/3
Case 1 :
f(x) = 1 - 3x
when x ≤ 1/3, f(x) is positive
Case 2 :
f(x) = -(1 - 3x)
when x > 1/3, f(x) is negative
Distributing negative, we get
f(x) = -1 + 3x or 3x - 1
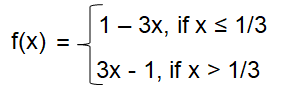
Problem 6 :
f(x) = |2x + 1|
Solution :
f(x) = |2x + 1|
f(x) = 2x + 1 and f(x) = -(2x + 1)
Let f(x) = 0
2x + 1 = 0
2x = -1
x = -1/2
Case 1 :
f(x) = 2x + 1
when x ≥ -1/2, f(x) is positive
Case 2 :
f(x) = -(2x + 1)
when x < -1/2, f(x) is negative
Distributing negative, we get
f(x) = -2x - 1

Problem 7 :
f(x) = x - |x|
Solution :
f(x) = x - |x|
Case 1 :
f(x) = x - x
f(x) = 0
Case 2 :
f(x) = x - (-x)
= x + x
f(x) = 2x
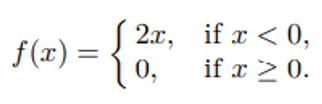
Problem 8 :
f(x) = x + |x - 1|
Solution :
f(x) = x + |x - 1|
Case 1 :
f(x) = x + x - 1
f(x) = 2x - 1
Case 2 :
f(x) = x + (-x + 1)
= x - x + 1
f(x) = 1
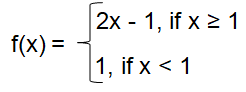
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling